WisFaq!

Examenopgave mbo 80-81 (3)

Ik krijg bij c. van deze examenopgave een vergelijking in x en y van het vlak door de x- en z-as. ik zou eigenlijk een vergelijking in x en z moeten krijgen toch? Kunt u kijken of ik dit goed doe?

Ten opzichte van een rechthoekig assenstelsel OXYZ zijn gegeven de A(4,0,0), B(4,5,0), C(0,6,0), D(-3,-2,0) en T(0,0,6).

1. Teken de piramide T·ABCD.
2. Bereken de coördinaten van het snijpunt van de lijnen AC en BD.
3. Bepaal een vectorvoorstelling van de snijlijn van het vlak door de punten C, D en T en het vlak door de x-as en z-as.

Ik heb mijn uitwerking ook opgestuurd.

mboudd
17-4-2020

Antwoord

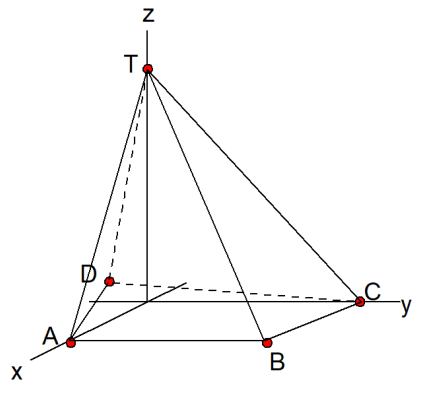
Voor het vlak door $C$, $D$ en $T$ krijg ik:

$
\eqalign{
& C = \left( {\matrix{
0 \cr
6 \cr
0 \cr

} } \right),D = \left( {\matrix{
{ - 3} \cr
{ - 2} \cr
0 \cr

} } \right),T = \left( {\matrix{
0 \cr
0 \cr
6 \cr

} } \right) \cr
& V_{CDT} = T + \lambda \cdot TD + \mu \cdot TC \cr
& V_{CDT} = T + \lambda \cdot \left( {D - T} \right) + \mu \cdot \left( {C - T} \right) \cr
& V_{CDT} = \left( {\matrix{
0 \cr
0 \cr
6 \cr

} } \right) + \lambda \cdot \left( {\left( {\matrix{
{ - 3} \cr
{ - 2} \cr
0 \cr

} } \right) - \left( {\matrix{
0 \cr
0 \cr
6 \cr

} } \right)} \right) + \mu \cdot \left( {\left( {\matrix{
0 \cr
6 \cr
0 \cr

} } \right) - \left( {\matrix{
0 \cr
0 \cr
6 \cr

} } \right)} \right) \cr
& V_{CDT} = \left( {\matrix{
0 \cr
0 \cr
6 \cr

} } \right) + \lambda \cdot \left( {\matrix{
{ - 3} \cr
{ - 2} \cr
{ - 6} \cr

} } \right) + \mu \cdot \left( {\matrix{
0 \cr
6 \cr
{ - 6} \cr

} } \right) \cr
& \left\{ \matrix{
x = - 3\lambda \cr
y = - 2\lambda + 6\mu \cr
z = 6 - 6\lambda - 6\mu \cr} \right. \cr
& (2) + (3) \cr
& \left\{ \matrix{
y + z = - 8\lambda + 6 \cr
x = - 3\lambda \cr} \right. \cr
& \left\{ \matrix{
3y + 3z = - 24\lambda + 18 \cr
8x = - 24\lambda \cr} \right. \cr
& (1) - (2) \cr
& - 8x + 3y + 3z = 18 \cr}
$

De vergelijking van het vlak door $x$- en $z$-as is $y=0$. Dan schiet het al lekker op...

Naschrift
Maar zo kan het natuurlijk ook:

$
\eqalign{
& C = \left( {\matrix{
0 \cr
6 \cr
0 \cr

} } \right),D = \left( {\matrix{
{ - 3} \cr
{ - 2} \cr
0 \cr

} } \right),T = \left( {\matrix{
0 \cr
0 \cr
6 \cr

} } \right) \cr
& V_{CDT} = C + \lambda \cdot CD + \mu \cdot CT \cr
& V_{CDT} = C + \lambda \cdot \left( {D - C} \right) + \mu \cdot \left( {T - C} \right) \cr
& V_{CDT} = \left( {\matrix{
0 \cr
6 \cr
0 \cr

} } \right) + \lambda \cdot \left( {\left( {\matrix{
{ - 3} \cr
{ - 2} \cr
0 \cr

} } \right) - \left( {\matrix{
0 \cr
6 \cr
0 \cr

} } \right)} \right) + \mu \cdot \left( {\left( {\matrix{
0 \cr
0 \cr
6 \cr

} } \right) - \left( {\matrix{
0 \cr
6 \cr
0 \cr

} } \right)} \right) \cr
& V_{CDT} = \left( {\matrix{
0 \cr
6 \cr
0 \cr

} } \right) + \lambda \cdot \left( {\matrix{
{ - 3} \cr
{ - 8} \cr
0 \cr

} } \right) + \mu \cdot \left( {\matrix{
0 \cr
{ - 6} \cr
6 \cr

} } \right) \cr
& \left\{ \matrix{
x = - 3\lambda \cr
y = 6 - 8\lambda - 6\mu \cr
z = 6\mu \cr} \right. \cr
& (2) + (3) \cr
& \left\{ \matrix{
x = - 3\lambda \cr
y + z = 6 - 8\lambda \cr} \right. \cr
& \left\{ \matrix{
8x = - 24\lambda \cr
3y + 3z = 18 - 24\lambda \cr} \right. \cr
& (1) - (2) \cr
& 8x - 3y - 3z = - 18 \cr}
$

WvR
17-4-2020