WisFaq!

Re: Re: Re: Constructies van vijfhoek en zeshoek

Dus er is een iets aan de hand als n (n-hoek) oneven en n even is. Hoe zullen we dat formuleren?

Hier komen bepaalde vragen aan de boord die ik nog niet begrijp.

1. Als wij veralgemeniseren: als er een n-hoek bestaat, hoe vinden we die dan?
   Dus hoe kunnen we bijvoorbeeld P1 synthetisch vinden, gegeven M1, M2, M3, ..., Mn?
2. En hoe hangt P1 algebraïsch af van M1, M2, M3, ..., Mn?
3. Of is P1 misschien vrij te kiezen (en voldoen er dus oneindig veel n-hoeken)?

Tot heden zie ik het nog niet. Graag jouw hulp daarvan. Alvast bedankt.

De groeten van M.

M
14-4-2020

Antwoord

n is oneven

Bij een oneven aantal middelpunten kan je een mogelijk beginpunt berekenen door de $x$ en $y$ om en om op te tellen en af te trekken. Hier bestaat een $P_1$, maar je kunt dat niet vrij kiezen.

Voorbeeld



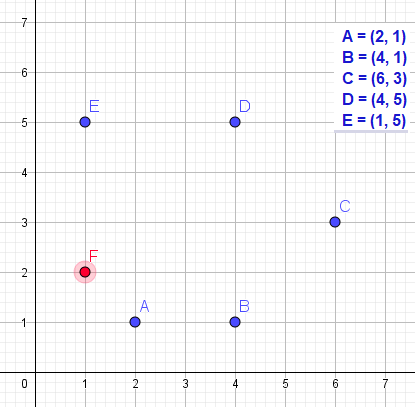
x = 2 - 4 + 6 - 4 + 1 = 1
y = 1 - 1 + 3 - 5 + 5 = 3

Dat punt $P_1$ moet dan (1,3) zijn.



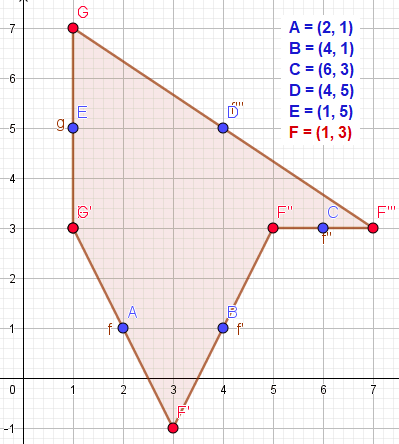
n is even

Ik vermoed dat bij een even aantal middelpunten die een zeshoek opleveren moet gelden dat de x en y bij optellen/aftrekking beide uitkomen op nul. Er is dus niet altijd een mogelijk beginpunt.

Voorbeeld



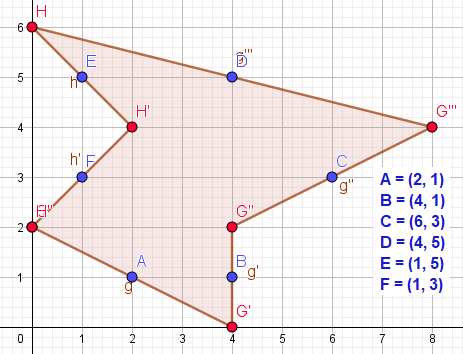
x = 2 - 4 + 6 - 4 + 1 - 1 = 0
y = 1 - 1 + 3 - 5 + 5 - 3 = 0

Maar dat laatste moet je dan nog aantonen!

Nu jij weer!

WvR
14-4-2020