WisFaq!

Re: Constructies van vijfhoek en zeshoek

Bedankt voor je uitleg. Alleen wil ik de coördinaten van de punten A t/m E behouden. Kan ik gewoon dezelfde strategie volgen? Of verandert er iets?

M
12-4-2020

Antwoord

Als je uit gaat van je oorspronkelijke tekening kan je dezelfde strategie volgen.



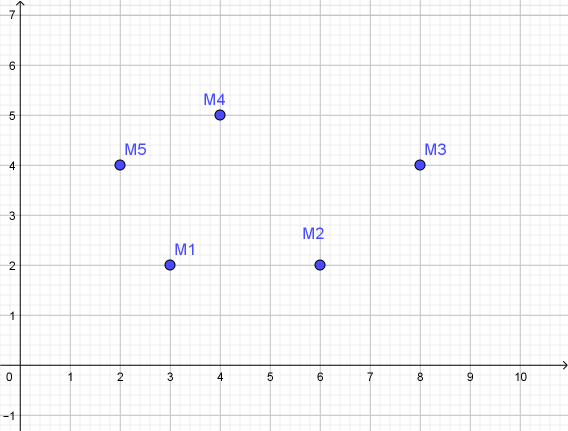
Je kunt het beginpunt ook berekenen!

$
\begin{array}{l}
M_1 (3,2) \\
M_2 (6,2) \\
M_3 (8,4) \\
M_4 (4,5) \\
M_5 (2,4) \\
P_1 (x,y) \\
\to M_1 (3,2) \\
P_2 (6 - x,4 - y) \\
\to M_2 (6,2) \\
P_3 (12 - (6 - x),4 - (4 - y)) \\
P_3 (6 + x,y) \\
\to M_3 (8,4) \\
P_4 (16 - (6 + x),8 - y) \\
P_4 (10 - x,8 - y) \\
\to M_4 (4,5) \\
P_5 (8 - (10 - x),10 - (8 - y)) \\
P_5 ( - 2 + x,2 + y) \\
\to M_5 (2,4) \\
P_1 \left( {4 - ( - 2 + x),8 - (2 + y)} \right) \\
P_1 \left( {6 - x,6 - y} \right) \\
\left\{ \begin{array}{l}
x = 6 - x \\
y = 6 - y \\
\end{array} \right. \\
\left\{ \begin{array}{l}
x = 3 \\
y = 3 \\
\end{array} \right. \\
P_1 (3,3) \\
\end{array}
$

Dat ziet er dan zo uit:



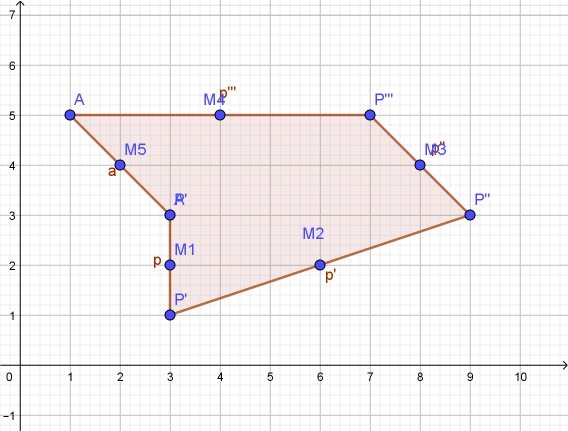
Dat kan vast op een handiger manier. Maar daar moet je dan maar 's zelf mee aan de slag. Wie weet wat er allemaal nog te ontdekken valt. Hopelijk kan je er verder mee...

Naschrift

Als $M$ het midden is van $AB$ dan geldt:

$
\eqalign{
& M = {{A + B} \over 2} \cr
& A + B = 2M \cr
& B = 2M - A \cr}
$

Als je coördinaten van $A$ en $M$ kent dan kan je de coördinatie van $B$ vinden met $
B = 2M - A
$

WvR
12-4-2020