WisFaq!

Examenopgave mbo 78-79 (2)

Ik heb hier en daar wat verschillen) met het model bij de volgen de examenopgave: (ruimte voor verbeteringen op of aanmerkingen zijn welkom)

Ten opzichte van een rechthoekig assenstelsel Oxyz zijn gegeven de punten A (4,-4,0), B(4,4,0), C (-4,4,0) en T (0,0,6). E is het midden van AT.

1. Teken de piramide T·ABCD.
2. Bepaal een vectorvoorstelling van vlak TAB.
   Ik heb (-4,-4,0)+l(0,1,0)+m(-4,8,6).
   Model heeft:(0,0,6)+l(2,2,-3)
3. Bepaal de vergelijking van vlak TDC
   Hier heb ik geen verschil met het model:
   3x-2z+12=0
4. Bepaal een vectorvoorstelling van een vlak $\alpha$ door E, zodanig dat vlak $\alpha$ evenwijdig is met vlak TDC.
   Hier heb ik een steunvector meer:
   (-2,-2,3)+r(2,2,3)+s(0,1,0) model geeft e(2,2,3)+w(-2,2,-3).
5. Bepaal een vectorvoorstelling van de snijlijn van vlak $\alpha$ en vlak TAB:
   Ik heb (12,0,6)+l(10,15,15).(zie mijn uitwerking)
   Het model geeft:(2,0,3)+l(0,1,0).
6. Bereken de hoek van de vlakken TAB en TDC.
   Ik heb een klein verschil ik zelf heb $\Phi$=0,36$\pi$
   model geeft $\Phi$=0,37$\pi$

Ik heb ook mijn hele uitwerking opgestuurd.

mboudd
8-4-2020

Antwoord

a.


b.
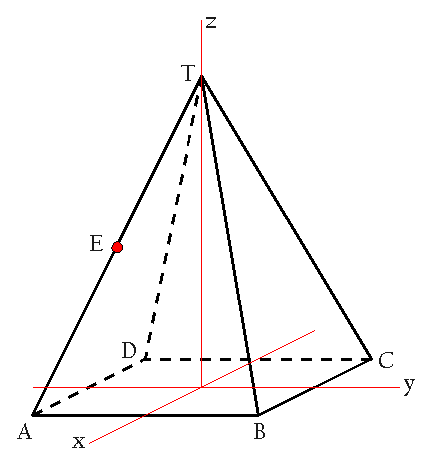
Dat model kan niet kloppen. Voor een vlak heb je in ieder geval twee richtingsvectoren nodig. Ik denk dat dit bedoeld was:

$
TAB:\left( {\matrix{
x \cr
y \cr
z \cr

} } \right) = \left( {\matrix{
0 \cr
0 \cr
6 \cr

} } \right) + \lambda \left( {\matrix{
2 \cr
{ - 2} \cr
{ - 3} \cr

} } \right) + \mu \left( {\matrix{
2 \cr
2 \cr
{ - 3} \cr

} } \right)
$

c.
Ok

d.
Je weet dat $\alpha$ evenwijdig is aan TDC.

$
\eqalign{
& E(2, - 2,3) \cr
& \alpha //TDC \cr
& \alpha :3x - 2z + d = 0 \cr
& 3 \cdot 2 - 2 \cdot 3 + d = 0 \cr
& d = 0 \cr
& \alpha :3x - 2z = 0 \cr
& O(0,0,0) \in \alpha \cr}
$

Ik weet dus al dat $O$ in het vlak $\alpha$ ligt. De vectorvoorstelling wordt dan (op de steunvector na) hetzelfde als die van het vlak TDC.

$
\alpha :\left( {\matrix{
x \cr
y \cr
z \cr

} } \right) = \rho \left( {\matrix{
2 \cr
2 \cr
3 \cr

} } \right) + \tau \left( {\matrix{
2 \cr
{ - 2} \cr
3 \cr

} } \right)
$

e.
De normaalvectoren van de twee vlakken staan loodrecht op de snijlijn. Je krijgt:

$
\eqalign{
& \overrightarrow n _{TAB} = \left( {\matrix{
3 \cr
0 \cr
2 \cr

} } \right) \cr
& \overrightarrow n _\alpha = \left( {\matrix{
3 \cr
0 \cr
{ - 2} \cr

} } \right) \cr
& \overrightarrow v _{snijlijn} = \left( {\matrix{
a \cr
b \cr
c \cr

} } \right) \cr
& \left( {\matrix{
3 \cr
0 \cr
2 \cr

} } \right) \cdot \left( {\matrix{
a \cr
b \cr
c \cr

} } \right) = 0 \Rightarrow 3a + 2c = 0 \cr
& \left( {\matrix{
3 \cr
0 \cr
{ - 2} \cr

} } \right) \cdot \left( {\matrix{
a \cr
b \cr
c \cr

} } \right) = 0 \Rightarrow 3a - 2c = 0 \cr
& a = 0\,\,en\,\,c = 0 \cr
& \overrightarrow v _{snijlijn} = \left( {\matrix{
0 \cr
1 \cr
0 \cr

} } \right) \cr}
$

Nu moet je alleen nog een steunvector zoeken. Ik denk er nog over na...

f.
Volgens mij moet het inderdaad $
\phi \approx {\rm{0}}{\rm{,37}}\pi
$ zijn.

$
\eqalign{
& \overrightarrow n _{TAB} = \left( {\matrix{
3 \cr
0 \cr
2 \cr

} } \right) \cr
& \overrightarrow n _{TDC} = \left( {\matrix{
3 \cr
0 \cr
{ - 2} \cr

} } \right) \cr
& \cos \phi = {{\left| {\left( {\matrix{
3 \cr
0 \cr
2 \cr

} } \right) \cdot \left( {\matrix{
3 \cr
0 \cr
{ - 2} \cr

} } \right)} \right|} \over {\left| {\left( {\matrix{
3 \cr
0 \cr
2 \cr

} } \right)} \right| \cdot \left| {\left( {\matrix{
3 \cr
0 \cr
{ - 2} \cr

} } \right)} \right|}} = {5 \over {13}} \cr
& \phi \approx {\rm{0}}{\rm{,37}}\pi \cr}
$

Je vergelijking voor TAB klopt niet!

Naschrift
De vergelijking van TAB:

$
\begin{array}{l}
TAB:\left( {\begin{array}{*{20}c}
x \\
y \\
z \\
\end{array}} \right) = \left( {\begin{array}{*{20}c}
0 \\
0 \\
6 \\
\end{array}} \right) + \lambda \left( {\begin{array}{*{20}c}
2 \\
{ - 2} \\
{ - 3} \\
\end{array}} \right) + \mu \left( {\begin{array}{*{20}c}
2 \\
2 \\
{ - 3} \\
\end{array}} \right) \\
\left\{ \begin{array}{l}
x = 2\lambda + 2\mu \\
y = - 2\lambda + 2\mu \\
z = 6 - 3\lambda - 3\mu \\
\end{array} \right. \\
\left\{ \begin{array}{l}
3x = 6\lambda + 6\mu \\
y = - 2\lambda + 2\mu \\
2z = 12 - 6\lambda - 6\mu \\
\end{array} \right. \\
(1) + (3) \\
3x + 2z = 12 \\
3x + 2z - 12 = 0 \\
\end{array}
$

WvR
9-4-2020