
In de R3 zijn er twee manieren om vlakken te beschrijven:
- Met een vergelijking
- Met een vectorvoorstelling
Vergelijking
Met een vergelijking in de ruimte geef je de relatie aan tussen $x$, $y$ en $z$. Neem bijvoorbeeld $x+y+z=4$. Je kunt bedenken dat bijvoorbeeld $(4,0,0)$ in dit vlak ligt. De punten $(0,4,0)$ of $0,0,4)$ liggen trouwens ook in dat vlak, maar ook punten als $(1,1,2)$ of $(0.-2,6)$... Als je maar zorgt dat $x+y+z=4$.
Vectorvoorstelling
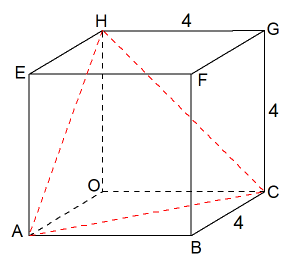
Dat vlak door A, C en H kan je ook aangeven met een vectorvoorstelling:
$
\left( {\begin{array}{*{20}c}
x \\
y \\
z \\
\end{array} } \right) = \left( {\begin{array}{*{20}c}
4 \\
0 \\
0 \\
\end{array} } \right) + \lambda \left( {\begin{array}{*{20}c}
{ - 1} \\
1 \\
0 \\
\end{array} } \right) + \mu \left( {\begin{array}{*{20}c}
{ - 1} \\
0 \\
1 \\
\end{array} } \right)
$
Wat is handig? Dat hangt er van af. Je kunt van de vergelijking van een vlak een vectorvoorstelling geven en je kunt van een vlak met een vectorvoorstelling een vergelijking geven.
Het voorvlak
Als vectorvoorstelling:
$
\left( {\begin{array}{*{20}c}
x \\
y \\
z \\
\end{array} } \right) = \left( {\begin{array}{*{20}c}
4 \\
0 \\
0 \\
\end{array} } \right) + \lambda \left( {\begin{array}{*{20}c}
0 \\
1 \\
0 \\
\end{array} } \right) + \mu \left( {\begin{array}{*{20}c}
0 \\
0 \\
1 \\
\end{array} } \right)
$
Als je nu probeert hiervan de vergelijking te geven dan kom je uit op $x=4$. Niet meer en niet minder...

Als je naar de tekening kijkt kun je ook zien dat dat niet zo gek is. Wat weet je van de punten in het voorvlak? Dat de $x$-co÷rdinaat gelijk aan 4 is, dus dan moet $x=4$ de vergelijking zijn. Je kunt voor $y$ en $z$ kiezen wat je wilt...
Vandaar die $x=4$ in de uitwerking. Je had natuurlijk ook de vectorvoorstelling van ABFE kunnen gebruiken om de co÷rdinaten van K te bepalen, maar mij leek $x=4$ wel zo handig...

WvR
27-2-2020