WisFaq!

Vergelijkingen bij meetkundige figuren

Dit is de opdracht:

Gegeven zijn de cirkel c1 met middelpunt M en straal 2 en cirkel c2 met middelpunt N en straal 1. De afstand tussen beide cirkels is 1. De gemeenschappelijke raaklijnen k en l snijden elkaar in het punt P. Zie het figuur wat ik stuur via de mail voor de plaatjes.

• Bereken exact sin(hoek(k,l))

Ik heb al NP gelijkgesteld aan x. Daarna heb ik vastgesteld dat driehoek MPD gelijk is aan driehoek NPC. Dit geeft:

MP/NP = MD/NC
(4 + x)/x = 2/1
2x = 4 + x
x = 4
dus NP = 4

Ik weet alleen niet meer wat ik hierna moet doen. Zouden jullie mij kunnen helpen. Alvast bedankt!

Sven
17-1-2020

Antwoord

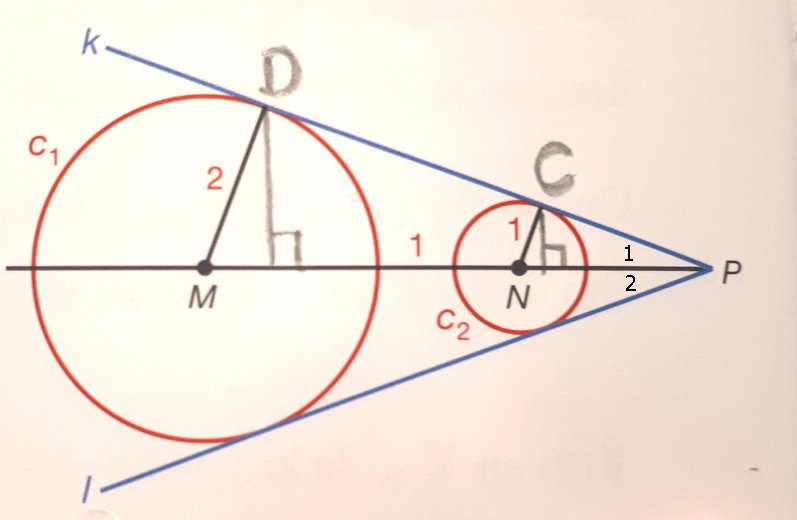
Je weet nu:

$
\eqalign{
& \sin \angle P_1 = \frac{1}
{4} \cr
& \cos \angle P_1 = \frac{\sqrt {15}}
{4} \cr
& \angle P_1 = \angle P_2 \cr}
$

De vraag is dan wat $
\sin \angle P
$ dan is...

In 't algemeen geldt:

$
\sin (2A) = 2\sin (A)\cos (A)
$

...en dan ben je er wel... Lukt dat?

WvR
17-1-2020