In de figuur links zie je een langwerpig houten blok met een driehoekige doorsnede. Aan de bovenkant wordt er een strook afgezaagd, rechts wordt er ook een strook afgezaagd. Je houdt dan een rechthoekige balk over, de 'kopse' kant van deze balk is blauw gekleurd.
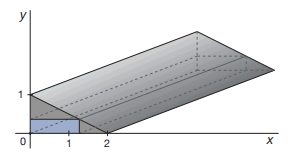
Je wilt dit doen op zo'n manier dat de balk zo veel mogelijk belasting kan dragen. Denk aan een situatie dat je de uiteinden op een steun legt, en je gaat in het midden op de balk zitten. De balk moet dan zo min mogelijk doorbuigen.
De blauwe rechthoek zou je heel breed kunnen kiezen (iets minder dan 2, breed is goed). Maar dan wordt de balk heel laag (dun), en dun is weer slecht: je kunt je voorstellen dat zo'n brede, maar heel dunne balk veel doorbuigt.
Je zou de balk ook heel smal kunnen kiezen. Dan is deze heel hoog (hoog is goed), maar ook heel smal, en smal is weer slecht. Een heel smalle balk buigt ook door. Het beste is dus ergens tussenin, en wij gaan berekenen wat de beste keuze is.
Nu kan je aantonen dat zo'n balk beter wordt wanneer bh2 groter wordt. We moeten proberen om bh2 zo groot mogelijk te maken, dat levert de beste balk op (meest belastbaar). Dit gaat als volgt:
Eerst stellen we een formule op die de bovenkant van het blok beschrijft. Dit is een rechte lijn door (0, 1) en door (2, 0). De formule is:
y = -1/2x + 1
Dit betekent: als we de breedte van de balk x kiezen, dan wordt de hoogte
-1/2x + 1.
Volgens de gegeven formule geldt dan:
D = b∑h2
D = x∑(-1/2x + 1)2
Haakjes netjes wegwerken:
D = 1/4x3-x2+x
We zoeken het maximum van D. Dan is de afgeleide nul:
D' = 0
3/4x2-2x+1 = 0
Met de abc-formule:
x=2/3 of x=2
x=2 voldoet niet, want daar is D juist minimaal. We vinden een maximale waarde bij x=2/3.
x is gelijk ook de breedte van de balk, dus:
b=2/3
De hoogte is dan:
h=-1/2∑2/3+1
h=2/3
Het maximaal dragend vermogen is dan:
D=bh2
D=2/3∑(2/3)2
D=8/27
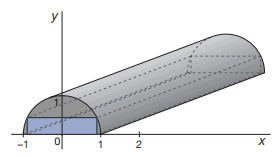
Voor de figuur rechts gaat het op dezelfde manier, alleen is de formule voor de bovenkant van je balk (de hoogte als functie van x) anders.
Lukt het zo?
GHvD
8-1-2020