WisFaq!

Re: Oorsprong naam parabool

Kan je dit misschien op een andere manier uitleggen? Ik heb dit bewijs ook nodig.

witze
3-1-2020

Antwoord

Spijtig dat je dit zelf niet hebt kunnen bewijzen, want het is nogal gemakkelijk.

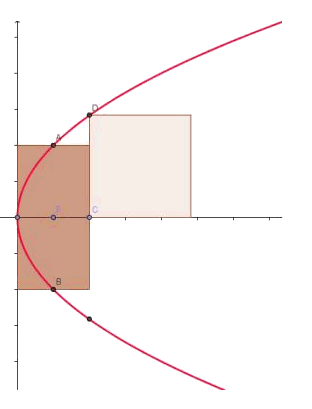
co(D) = (x,√2px) (punt op de parabool)
co(A) = (^p/₂,p) (punt op de parabool, loodrecht boven het brandpunt)

De zijde van het vierkant is de y-waarde van D, dus √2px.
De oppervlakte van het vierkant is dus z² = 2px

De breedte van de rechthoek is de x-waarde van D, dus x.
De halve hoogte is de y-waarde van A, dus p; de hoogte is dus 2p.
De oppervlakte van het rechthoek is b.h = x.2p = 2px
De oppervlakte van het vierkant en de oppervlakte zijn dus steeds (voor alle punten D op de parabool) gelijk.
Ok?

LL
3-1-2020