Natuurlijk kan dat bewezen worden (vragen naar de bekende weg?).
Ik teken eerst de vector $\vec{y} = \vec{a} - \vec{c}$
Omdat immers
$\vec{y} = \vec{a} + (-\,\vec{c})$
gaat dat eenvoudig met de diagionaalmethode.
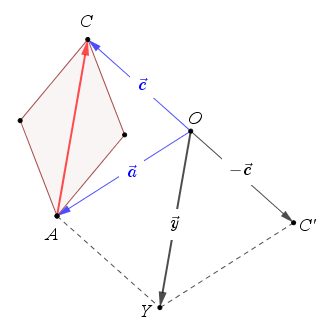
En ziet!... $\vec{y} \neq \vec{AC}$
want hun richtingen zijn tegengesteld. Wel is het zo, dat:
$OY // CA$ en $\|\,\vec{y}\,\| = \|\,\vec{AC}\,\|$
want $OCAY$ is (ook) een parallellogram.
Dus is (wel): $\vec{AC} = -\,(\vec{a} - \vec{c})$
Groet,
dk
3-1-2020