WisFaq!

Voor welke waarde van x zal de som kleiner zijn?

Hallo, ik heb een vraag over het oplossen van een ongelijkheid.



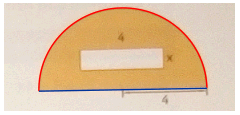
De vraag is: Voor welke waarde van x zal de som van de buitenomtrek en de binnenomtrek van de oranje figuur kleiner zijn dan 4$\pi$ + 20 eenheden?

Er wordt eerst gevraagd naar de formule voor de omtrek van de cirkel en dat begrijp ik helemaal. De formule is 2. $\pi$. r. Daarna vragen ze naar de formule voor de omtrek van de halve cirkel. Ik dacht dat dit dus gewoon bovenstaande formule gedeeld door 2 zou zijn. Dat is echter niet zo en het verwart me heel erg want ze geven als oplossing:

formule halve cirkel: ((2 $\pi$.4) : 2) + 2.4 = 4 $\pi$ + 8.

Maar vanwaar komt die 2x4, aub? Als men hier de binnenomtrek van de cirkel bedoelt, moet dit dan niet 2(x+4) zijn? Pas daarna, in de derde stap; wordt de omtrek van de rechthoek berekend en hier wordt dit wel: 2.(x+4)=2x+8.

De vergelijking wordt dan: 4 $\pi$+16+2x $<$ 4$\pi$+20
Ik begrijp hier niet waar die 16 (die extra 8 van die 2x4) vandaan komt? Kunt U dit uitleggen, aub?

Arthur
17-12-2019

Antwoord

Hallo Arthur,

Zie de figuur hieronder. De buitenomtrek van de oranje figuur is niet alleen de rode cirkelboog (lengte: 4$\pi$) maar ook het blauwe lijnstuk (lengte: 2·4=8):



De totale buitenomtrek is dus 4$\pi$+8.

De omtrek van de rechthoek is 4+x+4+x = 2x+8.

Opgeteld levert dit:

4$\pi$+8+2x+8 = 4$\pi$+16+2x

De ongelijkheid wordt dan:

4$\pi$+16+2x $<$ 4$\pi$+20
16+2x $<$ 20
2x $<$ 4
x $<$ 2

OK zo?

GHvD
17-12-2019