Geachte collega,
Graag stel ik de volgende vraag het gaat om machten en wortels, er komen verschillende antwoorden uit dit kan toch niet!
Bijvoorbeeld de zesdemachts wortel uit (-1)^2 = 1 dit klopt,
het zou gelijk moeten zijn aan (-1)^(2/6) maar hier komt -1 uit.
Mijn vraag hoe gaan we officieel om bij machten en negatieve grondtallen?Henk Lugers
28-11-2019
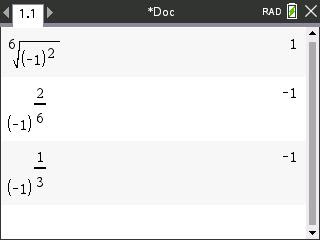
Het is een misvatting dat $\sqrt[6]{(-1)^2}$ en $(-1)^{\frac26}$ aan elkaar gelijk zouden moeten zijn. Het eerste is een samenstelling van twee bewerkingen: eerst kwadrateren en dan zesdemachtswortel nemen. Het tweede is één bewerking: een macht van $-1$ met een rationale exponent, en daar moet hetzelfde uitkomen ongeacht de manier waarop je dat getal representeert, dus $\frac13$, $\frac26$, $\frac{100}{300}$. $\dots$ moeten allemaal dezelfde uitkomst opleveren. Het meest voor de hand liggende is dan: eerst breuk vereenvoudigen en dan $\sqrt[n]{(-1)^t}$ waarbij $t$ en $n$ de teller en noemer zijn.
Voor negatieve grondtallen betekent dit dat een $q$-de macht niet altijd voorhanden is binnen de reële getallen, en dat maakt het opstellen van `officiële' regels wat lastig.
Binnen de complexe getallen is meer mogelijk, maar dan moet je rekening houden met het feit dat $(-1)^{\frac13}$ drie verschillende waarden heeft: $-1$, $\frac12\pm\frac12\sqrt3 i$ (en, nee, geen van die drie is uitverkoren de `echte' waarde te zijn).
Zie ook de onderstaande link naar de WiskundEbrief.Zie WiskundEbrief [http://www.wiskundebrief.nl/724.htm#4]
kphart
28-11-2019
#88725 - Rekenen - Docent
