WisFaq!

Extremumvraagstuk over sportstadion

Beste,

Ik heb de opdracht gekregen om het volgende extremumprobleem op te lossen. Ik ben nooit echt goed geweest in het oplossen van extremumproblemen en weet hier dus zo goed als niet hoe ik hier moet aan beginnen.

Een sportstadion bestaat uit een rechthoek, begrensd door 2 halve cirkelschijven. De omtrek van het stadion moet 400m bedragen.

• Hoe moeten de lengte l en de breedte b genomen worden, opdat de oppervlakte van het rechthoekig middelveld maximaal zou worden?

Wat ik weet: 200= b+l+r·$\pi$ en oppervlakte rechthoek= b·l
Alvast bedankt!

Phybe
25-9-2019

Antwoord

Maar een tekening en kies handige variabelen:



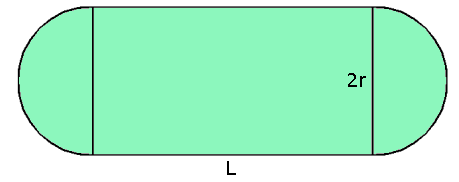
De lengte van het rechthoekig middelveld is $L$ en de straal van de twee halve cirkelschijven is $r$. De omtrek van het stadion is $2L+2\pi r$ en dat moet dan 400 meter zijn.

$2L+2\pi r=400$

De oppervlakte van het middelveld is gelijk aan $O=L·2r$ en dat moet dan zo groot mogelijk zijn. Om $O$ te maximaliseren is het handig om $O$ uit te drukken in één variabele.

Met de formule hierboven kan je $r$ uitdrukken in $L$ zodat je $O$ kan uitdrukken in $L$. De vraag wordt dan: wat moet je dan voor $L$ nemen om de oppervlakte zo groot mogelijk te laten zijn.

Zou dat lukken?

WvR
25-9-2019