WisFaq!

Wat is een kansverdeling?

Geachte

Hoe komen jullie aan de komma getalen bij het aantal ogen ( 4 dobbelstenen? Bij x₀ heb ik de berekening 5·5·5·5=625 en 6·6·6·6=1296 geeft 625/1296. Kom ik op 0.482 maar hoe gaat dat met x₁,x₂;x₃,x₄?

• Wat is een kansverdeling?

eveline
8-8-2019

Antwoord

Dat is een voorbeeld van een binomiale verdeling. Bij het voorbeeld met de munten krijg je:

$
P(X = 4) = \left( {\begin{array}{*{20}c}
8 \\
4 \\
\end{array}} \right) \cdot \left( {\frac{1}{2}} \right)^8 \approx 0,273
$

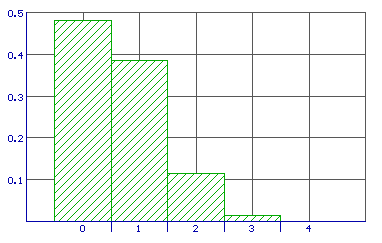
Bij de dobbelstenen krijg je:

$
\begin{array}{l}
P(X = 0) = \left( {\begin{array}{*{20}c}
4 \\
0 \\
\end{array}} \right)\left( {\frac{5}{6}} \right)^4 \left( {\frac{1}{6}} \right)^0 \approx 0,482 \\
P(X = 1) = \left( {\begin{array}{*{20}c}
4 \\
1 \\
\end{array}} \right)\left( {\frac{5}{6}} \right)^3 \left( {\frac{1}{6}} \right)^1 \approx 0,386 \\
P(X = 2) = \left( {\begin{array}{*{20}c}
4 \\
2 \\
\end{array}} \right)\left( {\frac{5}{6}} \right)^2 \left( {\frac{1}{6}} \right)^2 \approx 0,116 \\
P(X = 3) = \left( {\begin{array}{*{20}c}
4 \\
3 \\
\end{array}} \right)\left( {\frac{5}{6}} \right)^1 \left( {\frac{1}{6}} \right)^3 \approx 0,015 \\
P(X = 4) = \left( {\begin{array}{*{20}c}
4 \\
4 \\
\end{array}} \right)\left( {\frac{5}{6}} \right)^0 \left( {\frac{1}{6}} \right)^4 \approx 0,01 \\
\end{array}
$



Of heb ik iets gemist? Anders nog maar even vragen.

WvR
8-8-2019