Ik neem aan dat het de bedoeling is om een betrouwbaarheidsinterval te krijgen dat hoogstens 0,03 breed is. Je moet dan wel aangeven welke betrouwbaarheid je eist. Het meest gebruikelijk is een 95% betrouwbaarheidsinterval. De betekenis hiervan is: wanneer je met behulp van een steekproef een proportie (fractie) hebt bepaald, dan kan je met 95% betrouwbaarheid zeggen dat de proportie (fractie) van de gehele populatie binnen dit interval ligt.
De aanpak is als volgt:
Volgens de gegevens is uit een meting/onderzoek/steekproef/.... gebleken: de fractie 'tijdig uitgevoerde orders' is 204/240=0,85. Dat wil niet zeggen dat deze fractie voor alle mogelijke orders 0,85 is. Bij een volgende steekproef zou je best 0,86 of 0,82 kunnen vinden. Aangetoond kan worden dat de uitkomsten van veel steekproeven normaal verdeeld zijn. De uitkomst van een enkele steekproef kan je dus zien als één waarneming van een normaal verdeelde variabele.
De standaarddeviatie \sigma van deze verdeling vind je met de formule:
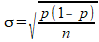
Hierin is:
p: populatieproportie 'tijdig geleverde orders'
n: lengte van de steekproef (dus: aantal orders dat je hebt onderzocht)
Lastig is dat je de populatieproportie niet kent, maar de steekproefproportie is een goede schatting, dus neemt men voor p de steekproefproportie.
Met n=240 en p=0,850 vinden we voor de standaardafwijking:
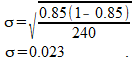
Een 95% betrouwbaarheidsinterval vinden we door vanuit de gevonden waarde 2 keer de standaardafwijking naar links te gaan, tot 2 keer de standaardafwijking naar rechts. (Eigenlijk 1,96 keer, maar omdat het bij dit soort statistische berekeningen altijd om schattingen gaat, hanteert men vaak 'keer twee' als vuistregel). Hier vinden we dus:
p-2\sigma = 0,850-2·0,023 = 0,804
p+2\sigma = 0,850-2·0,023 = 0,896
Het 95% betrouwbaarheidsinterval is [0,804 ; 0,896]
De breedte van het 95% betrouwbaarheidsinterval is dan:
0,896-0,804=0,092
(Omdat we vanuit p twee keer \sigma naar links gaan en twee keer \sigma naar rechts, kunnen we de breedte sneller uitrekenen door vier keer \sigma te nemen: 4·0,023=0,092)
Dit is te breed. We eisen:
4\sigma = 0,03
Dit kunnen we bereiken door een grotere waarde voor n te nemen. Deze berekenen we als volgt:
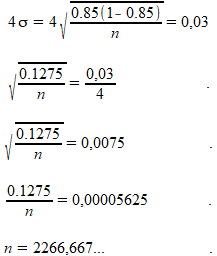
Uiteraard ronden we n af naar een geheel getal, en altijd naar boven omdat de steekproef anders net te klein zou zijn, met als gevolg een betrouwbaarheidsinterval dat net te groot zou zijn.
GHvD
16-6-2019