WisFaq!

Re: Ongelijkheden breuk oplossen

Goedenavond,

Ik weet dat -11 niet mee doet omdat je niet door 0 kan delen. Ik weet dat $x$ gelijk maar kleiner is dan 5.

$x$ is gelijk aan -3 en kleiner. Dit snap ik niet want als ik in de breuk de variabele $x$=-4 invul komt hier een positief getal uit.

Hassan
12-6-2019

Antwoord

De oplossing:

$
x < - 11 \vee - 3 \leq x \leq 5
$

Dus $x$=-4 hoort niet bij de oplossing. De breuk is dan groter dan $0$ inderdaad, dus dat klopt dan wel.

Had je gezien dat als de teller negatief is en de noemer postitief de breuk negatief is? In dat geval behoren die waarden voor $x$ tot de oplossing. De breuk moest immers kleiner of gelijk aan nul zijn. Zo zijn er nog wat mogelijkheden. Voor elke gebied moet je kijken hoe 't zit.

In het tekenverloop kan je zien waar de teller en de noemer negatief dan wel postief is. Je weet dan of de breuk negatief (die getallen voldoen) dan wel postitief is en die horen dan niet bij de oplossing.



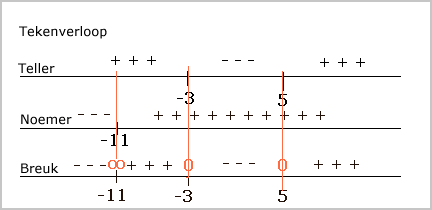
De nulpunten van de teller en de noemer spelen daarbij een belangrijke rol. Bereken de nulpunten van teller en noemer. Stel een tekenverloop van de teller en een tekenverloop van de noemer op en kijk naar de deling.

Meer moet het niet zijn.

• Ongelijkheden oplossen

WvR
12-6-2019