WisFaq!

Re: Maximale manteloppervlakte cilinder

Bedankt! Dat had ik inderdaad nog niet gezien maar ik snap niet goed hoe de stelling van Pythagoras in dit vraagstuk kan helpen.

Marie
9-6-2019

Antwoord

Met $r$, $x$ en $h$ krijg je:



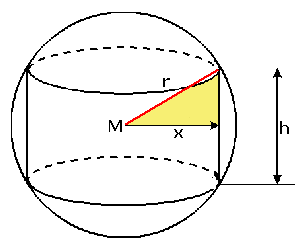
In het gekleurde driehoekje geldt:

$
x^2 + \left( {\frac{1}
{2}h} \right)^2 = r^2
$

Daarmee kan je $h$ uitdrukken in $x$.

De oppervlakte van de cilindermantel is gelijk aan:

$
O_{cilindermantel} = 2\pi x h
$

Met deze uitdrukking kan je de oppervlakte van de cilindermantel uitdrukken in $x$. Zou het dan lukken?

WvR
9-6-2019