Als ik het goed begrijp, ben je op zoek naar een formule om de inhoud van een 'cakevorm' te berekenen. Ik ga uit van een vorm waarvan het grondvlak rechthoekig is met zijden a en b, het bovenvlak is een rechthoek met zijden c en d. De hoogte is h:
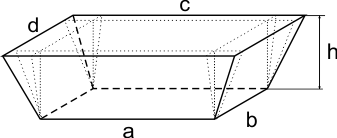
Deze figuur is op te delen in enkele standaard figuren, zie de stippellijnen in bovenstaande figuur. Centraal vinden we een balk met afmetingen a, b en h:
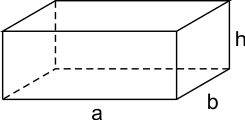
De inhoud van deze balk is a·b·h.
Langs de zijden met lengte a vinden we twee wigvormige figuren. Deze schuiven we denkbeeldig tegen elkaar, we vinden een driehoekig prisma:

De inhoud van dit prisma is 1/2(d-b)·a·h.
Langs de andere zijde van de balk vinden we eenzelfde soort prisma:
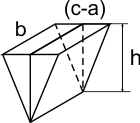
De inhoud hiervan is 1/2(c-a)·b·h.
Tot slot vinden we op de hoeken vier piramides. Ook deze kunnen we tegen elkaar schuiven tot één grotere piramide met een grondvlak van (c-a)x(d-b) en hoogte h. De totale inhoud hiervan is 1/3(c-a)(d-b)·h.
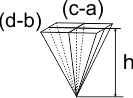
Wanneer je al deze inhouden optelt en een beetje herschrijft, dan vind je als formule:
Totale inhoud is 1/6(2ab + 2cd + ad + bc)·h
Er is niet een eenduidige oplossing voor jouw vraag: je geeft niet aan hoe schuin de opstaande zijden zijn (ik neem aan dat h 1 meter blijft). Wanneer deze opstaande zijden (bijna) verticaal zijn, dan zijn a en c (bijna) de oorspronkelijke 7.5 meter, b en d zijn (bijna) de oorspronkelijke 2 meter. Hoe schuiner de wanden, hoe meer a en b afnemen en c en d toenemen.
GHvD
17-3-2019