WisFaq!

Differentiaalvergelijkingen

Goed avond,
Ik tracht via een 0substitutie differentiaalvergelijkingen op te lossen. Ik tracht zo met een DV te komen staan met te scheiden variabelen. Maar ik kom er alleen uit voor a)(gewone oplossing en scheiden variabelen) uit maar b) niet.0
a) y'=x²/(1-y) of dy=x²/(1-y)dx
b)y'=xy/(x+y)

Voor de eerste gebruikte ik scheidning variabelen.:
a) (1-y)dy=x²dx
dy-ydy=x²dx
y-y²/2= x³/3 +C

b) hier gebruikte ik de substitutie xy= v en ook x+y=t maar
y'=xy/(x+y)
Voorbeeld
xy=v of y=v/x en dy= xdv-vdx
xdv-vdx= v/(x+v/x)
xdv-vdx=((vx)/(x²+v))dx (x²+v) is niet nul
xdv-vdx=(vx)dx/(x²+v)
x³dv+vxdv-vx²dx-v²dx=vxdx

Poging x+y=t lukte ook niet.

Men vraagt dan ook voor iedere vergelijking hetsveld in en (x,y)stelsel weer te geven.
Hier geraak ik vast....
Welke substitutie zouden jullie mij aanraden ? En hoe teken ik die grafieken?
Of moet er iets anders gebeuren?
Groetjes

Rik Lemmens
5-1-2019

Antwoord

De tweede vergelijking lijkt geen `mooie' oplossing te hebben; Maple geeft geen oplossing in formulevorm.

Hier is een plaatje van het richtingsveld van die vergelijking:



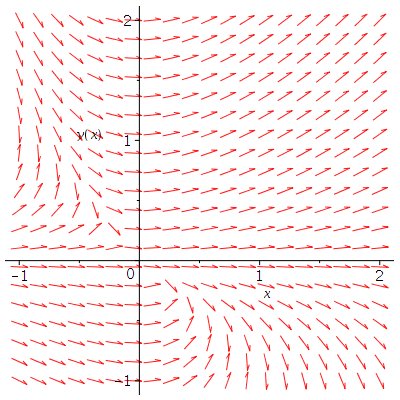
Daaraan kun je zien wat het kwalitatieve gedrag van de oplossingen is.

Je maakt het door in een (groot) aantal punten een pijltje te tekenen met helling $y'(x)$ en dat is dus $xy/(x+y)$.

kphart
6-1-2019