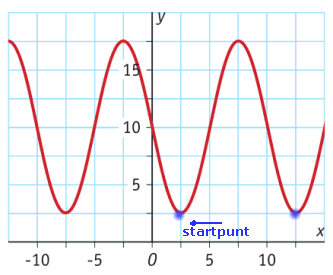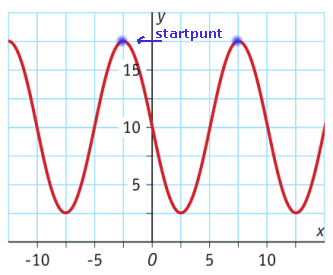
WisFaq!

Als b<0 moet zijn...

Bij opdracht 2b staat: geef de waarde van a,b,c en d voor y a+bcos(c(x-d)) voor b$<$0.

Moet dat niet zijn (net als antwoord a) maar dan alles $-$ dus:
Y=10-7,5 sin($\pi$/5(x+5))

• als b<0 moet zijn

Mboudd
22-12-2018

Antwoord

Nee. De evenwichtsstand en de amplitude veranderen niet. Wat er verandert is het 'startpunt'... en 't was cosinus toch?

$ y = 10 + 7\frac{1} {2}\cos \left( {\frac{1} {5}\pi \left( {x + 2\frac{1}{2}} \right)} \right) $	$ y = 10 - 7\frac{1} {2}\sin \left( {\frac{1} {5}\pi \left({x-2\frac{1}{2}}\right)} \right) $

Als $b$<$0$ dan begin je bij opdracht 2b op het laagste punt. Je moet de opgaven niet door elkaar halen...:-)

WvR
22-12-2018