WisFaq!

Meetkundige plaats snijpunt van twee variabele rechten

Graag had ik jullie hulp ingeroepen bij volgend probleem, dat te maken heeft met het zoeken van een meetkundige plaats, maar uiteindelijk wordt teruggebracht naar het aantonen dat twee hoeken gelijk zijn.

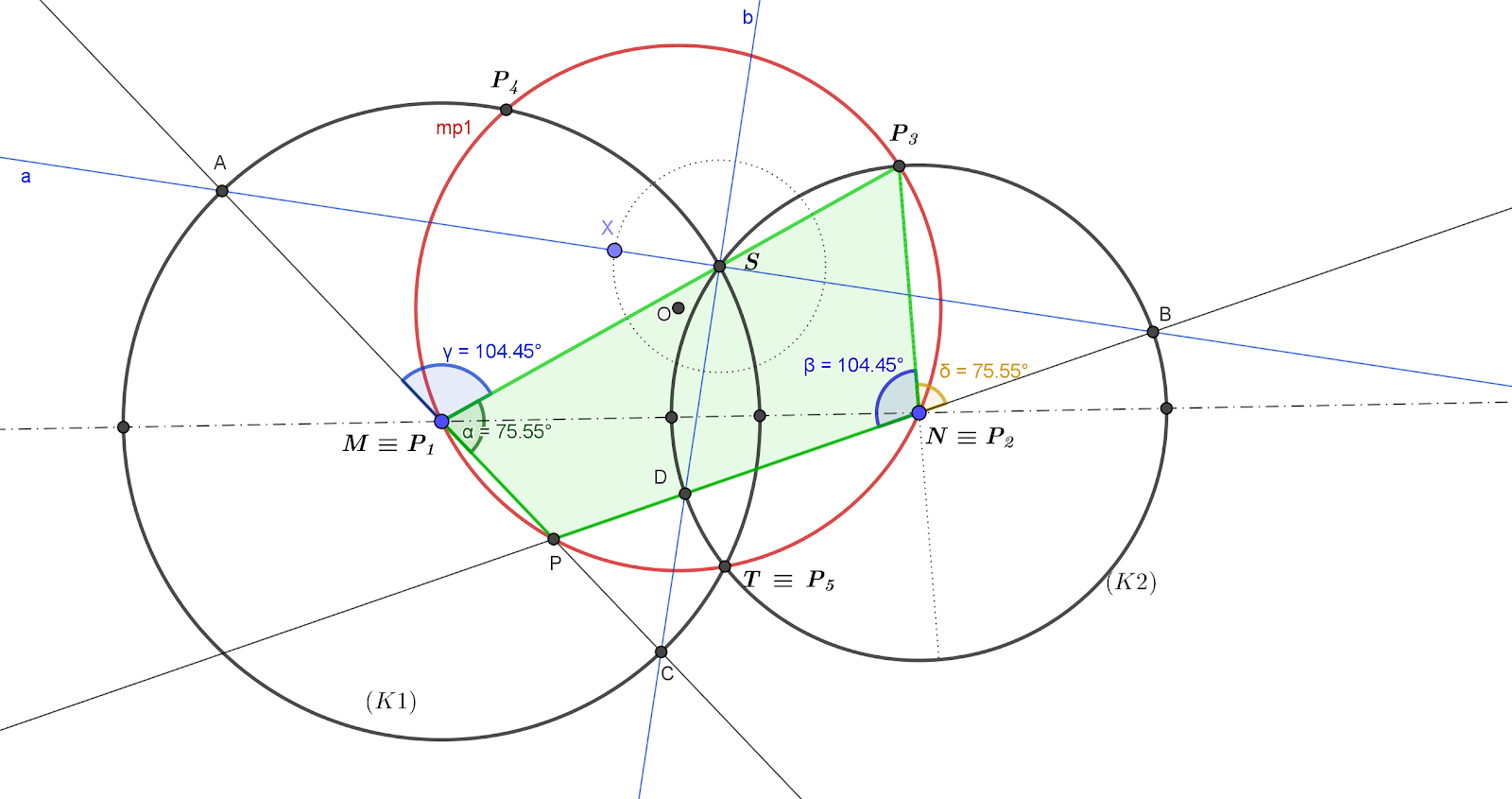
De opgave: Gegeven zijn de cirkels M en N, die elkaar snijden in S en T. Een rechte a door S snijdt de cirkel M resp. de cirkel N in A resp. B. De loodlijn b op a in S snijdt cirkel M resp. cirkel N in C resp. D. Bepaal de meetkundige plaats van het snijpunt P van de rechten AC en BD als a rond S draait.

Klik voor een vergroting

Door enkele bijzondere standen van de rechte a te kiezen (o.a. a gaande door M resp. N; a evenwijdig met MN; a rakend in S aan de cirkel M resp. cirkel N) kwam ik tot een vijftal bijzondere snijpunten P1 t/m P5, die zeker deel zullen uitmaken van de gezpchte meetkundige plaats. Ze zijn terug te vinden op bijgaande figuur, maar de constructielijnen werden achterwege gelaten om de tekening niet te overladen.

Ik richtte dan de focus op de punten P1=M, P2=N, P3 en P (snijpunt van AC en BD). Mijn idee is nu om aan te tonen dat de vierhoek P1P3P2P een koordenvierhoek (lichtgroene kleur) is, dan is aangetoond dat P op een cirkel moet liggen met een vaste koorde MN.

Hiervoor is nodig dat kan worden aangetoond dat de hoek(AMS) = hoek(P3NP) (1) of als alternatief aantonen dat de hoek(PMS) = hoek(P3NB) (2). Twee overstaande hoeken in de vierhoek P1P3P2P zijn dan in som 180°, wat dan ook geldt voor het andere paar overstaande hoeken in dezelfde vierhoek.

Via berekening met de tool GeoGebra stelde ik de gelijkheid vast van (1) en (2). Maar da's geen bewijs natuurlijk, maar het bracht mij wel op de idee om zo te werk te gaan.

VRAAG:
Kan u mij helpen met een hint om aan te tonen dat hetzij de gelijkheid (1) of eventueel de gelijkheid (2) wel degelijk algemeen geldig is? Bij voorbaat hartelijk dank!

Jan Heyndrikx
1-7-2018

Antwoord

Beste Jan,

Ik ga er van uit dat je hebt aangetoond dat $S$ op $MP_3$ ligt.

Als dat zo is, dan heb ik het volgende:

$\angle CAS = \angle MAS = \angle MSA$ (gelijkbenige driehoek) $=\angle P_3SB = \angle P_3DB$ (constante hoekstelling) $= \angle P_3DN = \angle DP_3N$ (gelijkbenige driehoek).

En tevens:

$\angle SBD = \angle SP_3D$ (constante hoekstelling).

Dus $\angle MP_3N = \angle SP_3N = \angle SP_3D + \angle DP_3N = \angle CAS + \angle SBD = \angle PAB + \angle ABP$.

Nu is snel te zien dat $\angle MP_3N + \angle NPM = 180^\circ$, want is om te schrijven tot de hoekensom van $\Delta ABP$.

Groeten,

FvL
10-7-2018