WisFaq!

Oefenen met integraal

Beste,

Tijdens het oefenen voor mijn tentamen kwam ik de volgende integraal tegen:

$\int{}$^3x-5/_x+1 dx.

Toen ik er niet uitkwam heb ik WolframAlpha geraadpleegd. Hier kwam een stappenplan uit (u ziet het stappenplan in de mail voor de plaatjes). U ziet dat daar op het einde een +3 wordt toegevoegd. Echter zie ik niet in waarom deze moet worden toegevoegd.

Om naar een antwoord te zoeken heb ik beide integranten geplot en hierbij kwamen de twee grafieken uit (wederom bij de mail toegevoegd). Ik zag dat dankzij de +3 e gehele grafiek positief is geworden. Heeft dat er iets mee te maken?

Ik hoop dat u mij hierbij kunt helpen. Bij voorbaat dank.

Erwin

Erwin den Boer
1-4-2018

Antwoord

Hallo Erwin,

WolframAlpha geeft als oplossing:



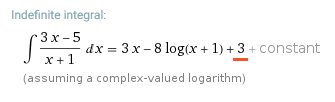
Ik vermoed dat deze +3 als volgt tot stand komt:

De te integreren functie wordt omgevormd, zodat we krijgen:
$\int{}$^(3x-5)/_(x+1)dx = $\int{}$3-⁸/_(x+1)dx

Vervolgens wordt substitutie toegepast: u=x+1 (en dus: dx=du). Dit levert:
= $\int{}$3-⁸/_(u)du

Integreren levert dan als primitieven:
= 3u-8ln|u|+C

Nu weer terug-substiteren:
= 3(x+1)-8ln|x+1|+C

Haakjes wegwerken levert:
= 3x+3-8ln|x+1|+C
= 3x-8ln|x+1|+3+C

Echter, 3+C levert een nieuwe constante op, die kunnen we C₂ noemen. Hiermee komen we op een vereenvoudigd eindresultaat:

$\int{}$^(3x-5)/_(x+1)dx = 3x-8ln|x+1|+C₂

Het enige verschil met de oplossing van WolphramAlpha is dat onze uiteindelijke constante C₂ niet dezelfde waarde heeft als de oorspronkelijke integratieconstante C direct na het integreren. Het is een formaliteit, maar toch: het zou relevant kunnen zijn wanneer je vóór het terug-substitueren aan de hand van randvoorwaarden al een waarde aan C zou toekennen. In dat geval zou je deze waarde niet klakkeloos kunnen overnemen na het terug-substituren.

Doorgaans zal je pas na terug-substitutie een waarde voor de integratieconstante bepalen, dan werk je gewoon met de nieuwe constante C₂ en is de waarde van de tussenliggende C niet van belang.

Opmerking:

Wanneer we 'met de hand' integreren, zouden we de integraal natuurlijk opsplitsen:

$\int{}$3-⁸/_(x+1)dx = $\int{}$3dx - 8$\int{}$¹/_(x+1)dx

Bij de eerste integraal passen we dan geen substitutie toe. Een computer werkt vaak anders dan een mens.
We krijgen dan wel voor beide integralen een integratieconstante (bv C₁ en C₂) die we ook weer kunnen samenvoegen tot een nieuwe constante C₃=C₁+C₂

GHvD
1-4-2018