WisFaq!

Complexe getallen

Als f(z)=z² is het reële deel u(x,y)=x²-y² en het imaginaire deel v(x,y)=2xy dat begrijp ik maar als f(z)= (abs z)² met abs is de absolute waarde van z dan is het reële deel van f u(x,y)=x²+y² dat snap ik maar waarom is het imaginaire deel v(x,y)=0? Want als z = x+jy dan is (abs z) = (abs x+jy)² = x² +y²+2xyj waarom is v(x,y) dan niet gelijk aan 2xy?

Arne Delafaille
30-3-2018

Antwoord

Hallo Arne,

De absolute waarde van een complex getal is als volgt gedefinieerd:



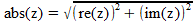
In het complexe vlak is dit de afstand van de oorsprong tot het betreffende punt, net zoals de absolute waarde van een reëel getal de afstand is van 0 tot dit getal op de getallenlijn.

Uiteraard levert links en rechts kwadrateren:

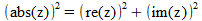
Zie Wikipedia: absolute value complex numbers [https://en.wikipedia.org/wiki/Absolute_value#Complex_numbers]

GHvD
30-3-2018