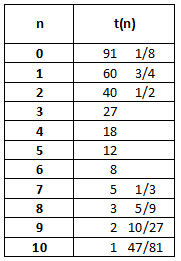
Er geldt:
$
t_n = t_0 \cdot r^n
$
Voor $t_4=18$ geldt dan:
$
\eqalign{18 = t_0 \cdot \left( {\frac{2}
{3}} \right)^4}
$
Los de vergelijking op en je weet de waarde van $t_0$. Met de waarde van $t_0$ kan je dan (vrij eenvoudig) de waarde van $t_1$ uitrekenen.
Op meetkundige rijen staat ook de formule voor de som van een meetkundige rij:
$
\eqalign{\sum\limits_{k = 0}^n {t_k } = \frac{{t_0 - t_{n + 1} }}
{{1 - r}}}
$
Voor $s_8$ geeft dat:
$
\eqalign{s_8 = \frac{{t_0 - t_9 }}
{{1 - \frac{2}
{3}}}}
$
Vul $t_0$ en $t_9$ in en je bent er uit!
Zou dat lukken?
Lees je de spelregels nog even!
WvR
29-3-2018