$
\eqalign{
& a = 1,067 \cr
& b = 4000 \cr
& X_{t + 1} = 1,067X_t + 4000 \cr}
$
Zodat:
$
\eqalign{
& X_t = \frac{{4000}}
{{1 - 1,067}} + \left( {0 - \frac{{4000}}
{{1 - 1,067}}} \right) \cdot 1,067^t \cr
& X_{15} = {\text{98}}{\text{.224}} \cr}
$
Dat is dan postnumerando. Voor prenumerando moet je nog delen door $1,067$ en dan kom je uit op een eindbedrag van $92.056$.
Zoiets kan je ook met Excel doen:
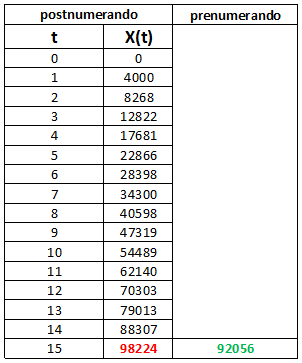
Naschrift
Ik zag dat men soms de laatste termijn niet in de berekening wordt meegenomen. Dat is niet handig, maar in dat geval zou je uit komen op $94.224$ en $88.307$. Dat moet je dan nog maar 's navragen bij je docent.
Zie Wat is een annu´teit? [http://www.wisfaq.nl/showrecord3.asp?id=86012]
WvR
30-3-2018