WisFaq!

Eigenschappen sommatieteken

Hallo,
In een voorbeeldtoets ben ik een meerkeuzevraag tegengekomen die ik helemaal niet snap. Er wordt namelijk gevraagd aan wat het volgende gelijk is: het sommatieteken met k=2 en n=2015 van (k/(k+1)) MIN het sommatieteken met k=2 en n=2015 van (k-1)/k.
Het antwoord is: 2015/2016-1/2
Mvg

Anon
30-1-2018

Antwoord

Je kunt de reeksen een stukje uitschrijven:

$
\eqalign{
& A:\frac{2}
{3} + \frac{3}
{4} + \frac{4}
{5} + ... + \frac{n}
{{n + 1}} \cr
& B:\frac{1}
{2} + \frac{2}
{3} + \frac{3}
{4} + ... + \frac{{n - 1}}
{n} \cr}
$

Als je nu $B$ van $A$ aftrekt valt bijna alles tegen elkaar weg, behalve de laatste term van $A$ en de eerste term van $B$.

Je weet $n=2015$ en dan ben je er wel. Helpt dat?

Naschrift

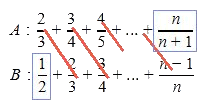
WvR
30-1-2018