Je mag altijd kiezen welke formule je gebruikt: beide formules stellen dezelfde algemene kwadratische formule voor. Werk maar eens de haakjes weg bij de volgende twee formules, je zult zien dat je twee keer hetzelfde resultaat krijgt:
y=2(x-3)2-8
y=2(x-1)(x-5)
Maar het kan wel handig zijn om de ene formule te gebruiken of juist de andere.
De eerste formule y=a(x-p)2+q is vooral handig wanneer je gegevens hebt over de top van de grafiek, of om een andere reden veel met deze top wilt werken. Immers, p en q zijn de coördinaten van de top van de grafiek.
De formule y=a(x-d)(x-e) is juist handig wanneer je de snijpunten van de grafiek met de x-as kent (de nulpunten) of veel met deze punten wilt werken. Want: d en e zijn de x-coördinaten van deze snijpunten.
Ik geef twee voorbeelden:
Welke formule hoort bij de onderstaande grafiek? De top ligt op (3, -4) en de grafiek gaat door (5, 12).
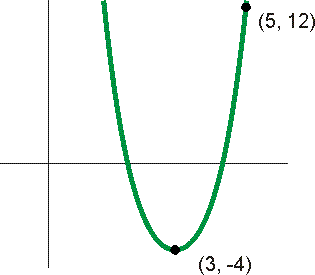
Je weet niets over snijpunten met de x-as, je kent wel de top. We gebruiken dus:
y = a(x-p)2 + q
Coördinaten top invullen:
y = a(x-3)2 - 4
Om a te vinden, vullen we één bekend punt in. Hier is dit x=5, y=12:
12 = a(5-3)2 - 4
aˇ22 - 4 = 12
4a = 16
a = 4
Dus de gevraagde formule is:
y = 4(x-3)2 - 4
Voorbeeld 2:
Welke formule hoort bij de onderstaande grafiek? De grafiek gaat door (2, 0), (4, 0) en (5, 12).
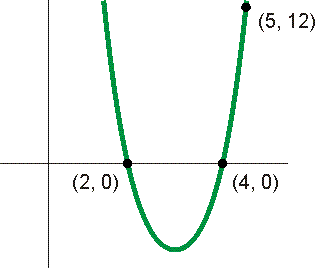
Nu weten we niets over de top, we kennen wel de snijpunten met de x-as. We gebruiken dus:
y = a(x-d)(x-e)
Coördinaten nulpunten invullen:
y = a(x-2)(x-4)
Om a te vinden, vullen we één bekend punt in. Hier is dit x=5, y=12:
12 = a(5-2)(5-4)
12 = aˇ3ˇ1
3a = 12
a = 4
Dus de gevraagde formule is:
y = 4(x-2)(x-4)
Het is je misschien opgevallen dat de twee grafieken hetzelfde zijn. Alleen hebben we andere gegevens over de grafiek, daarom hebben we verschillende formules gekozen. Maar als de grafieken hetzelfde zijn, dan moeten de gevonden formules ook hetzelfde zijn. Werk de haakjes maar eens weg, dan zal je zien dat dit inderdaad het geval is!
Zie ook Hoe kun je de formule van een parabool vinden?
GHvD
21-1-2018