WisFaq!

Uitzwenking voertuig in boog

Een (trein)wagon is 30 cm lang, daarvan is 21,6 cm de koorde (stuk tussen de draaistelassen), en 4,2 cm het starre deel aan de kopse kanten (er zijn 2 kopse kanten). De overhang van de wagon aan de binnenzijde van de boog, begrijp ik. Dat is de pijl, uitgedrukt in koorde en radius.

Maar de uitzwenking niet: De kopse kanten van de wagonbak steken uit t.o.v. de snijpunten van de koorde.

De uitzwenking is het verlengde van de boogstraal (dus buiten de boog) tot aan het verlengde van de koorde.

• Hoe druk ik de uitzwenking uit in radius, koorde en kopmaat?

jw
20-1-2018

Antwoord

Beste JW,

Eerst maar even een schets maken (niet op schaal):



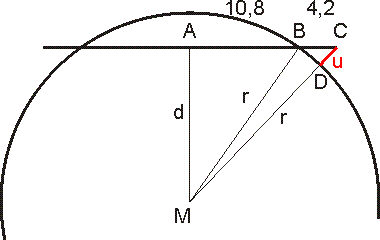
Het lijnstuk AC stelt een halve wagon voor, op een gebogen rail met radius r. Ik begrijp dat de lengte van de wagondelen buiten de draaistelassen de kopmaat wordt genoemd, deze is hier 4,2 cm (lijnstuk BC). De halve lengte tussen de draaistelassen is 10,8 cm (lijnstuk AB). Ik begrijp dat je de lengte van het lijnstukje u wilt weten (lijnstuk DC).

In driehoek MBC geldt volgens pythagoras:

d²+10,8²=r²

dus:

d² = r²-10,8²

d² = r²-116,64 (vergelijking 1)

In driehoek MCA geldt:

(r+u)² = d²+15²

(r+u)² = d²+225 (vergelijking 2)

Vergelijking 1 vullen we in vergelijking 2 in:

(r+u)² = r²-116,64+225
(r+u)² = r²+108,36

Links en rechts wortel trekken:

r+u = √(r²+108,36)

Zodat:

u = √(r²+108,36) - r

Hierbij gaat het natuurlijk om de uitzwenking van de hartlijn van de wagon. Door de breedte van de wagon steekt deze verder uit.

OK zo?

GHvD
20-1-2018