WisFaq!

Suikervraagstuk

Beste,

De massa X van de dozen suiker (van 1kg) van een suikerfabrikant is normaal verdeeld N (u en sigma = 10g). Regelmatig controleert men de massa van deze dozen aan de hand van een willekeurige steekproef van 20 dozen.

• Bepaal de gemiddelde massa u dat een doos moet hebben opdat bij de controle de kans om minstens één doos met een massa kleiner dan 1 kg te vinden, slechts 0,1 procent zou bedragen.

Ik was bezig met herhalingsoefeningen tot ik plots vast kom te zitten met deze oefening. Ik zou het enorm appreciëren als iemand me kon helpen.

MVG
Jaris

jaris
28-5-2017

Antwoord

Hallo Jaris,

• De doet 20 keer een waarneming (massa meten),
  
• Steeds zijn maar twee uitkomsten mogelijk: succes (massa is voldoende) of mislukking (massa is onvoldoende),
  
• De kans op succes (en dus op mislukking) is constant,
  
• Je let op het aantal keer succes (of aantal keer mislukking).

Dit zijn typisch kenmerken van een binomiale kansverdeling. In jouw geval moet je eerst oplossen:

Bepaal p_mislukking zodanig dat p(aantal mislukkingen$\ge$1)=0,001.

Volgens de complementregel geldt:
p(aantal mislukkingen$\ge$1) = 1-p(aantal mislukkingen=0)
ofwel:
p(aantal mislukkingen$\ge$1) = 1-p(aantal succes=20)

We moeten dus vinden:
1-p(aantal succes=20)=0,001
p(aantal succes=20)=0,999

De kans op 20 keer succes is (p_succes)²⁰, dus moet gelden:

(p_succes)²⁰=0,999
p_succes=0,999^1/20

Vanaf nu is de vraag: wat moet de gemidddelde massa van dozen suiker zijn, opdat de kans dat een willekeurige doos zwaarder is dan 1 kg gelijk is aan 0,999^1/20?

Maak bij vragen over de normaalverdeling altijd een schets. Bij deze vraag ziet die er zo uit:



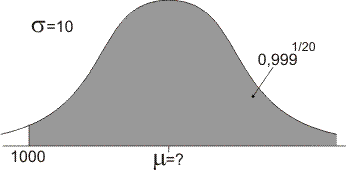
Ik vind een gemiddelde waarde van 1038,9 gram, jij ook?

GHvD
28-5-2017