WisFaq!

Re: Re: Re: Re: Re: Bol in een kegel

Hoi Gilbert,

Ik krijg dan uit h = 0 of h = -2. Ik vermoed dat ik dan de fout inga bij de afgeleide. Klopt het dat als je de gegevens invult in de formule van de inhoud dat je de volgende formule uitkrijgt na herleiden? 1/3pi · h² · r₂ (:) (h-2r). Hierdoor krijg ik een afgeleide, maar kom dan alsnog op het foute antwoord uit.

Didier
13-5-2017

Antwoord

Hallo Didier,

De formule voor de inhoud van je kegel is correct:



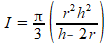
Kennelijk gaat er iets mis met differentiëren of herleiden.
Tussen haakjes staat een quotiënt. De teller noem ik even t, de noemer is n. Ik bereken ook alvast de afgeleide t' van de teller en de afgeleide n' van de noemer naar h, dus:



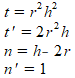
De afgeleide Q' van zo'n quotiënt bereken je met de quotiëntregel:



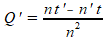
De afgeleide I' van de inhoud wordt hiermee:



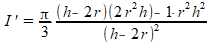
We zoeken de waarde van h waarvoor I'=0. Voldoende is om de teller van de breuk gelijk aan nul te stellen. Het herleiden gaat dan als volt:



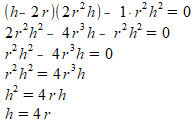
Kan je zelf vinden waar jouw berekening mis ging?

GHvD
13-5-2017