WisFaq!

Re: Smartie in vierkant

Ik (Onno) realiseer me dat we (samen met de studenten) niet duidelijk zijn. We weten wel L maar we weten niet a en b.
Kunnen we a en b bepalen? Als dat niet kan kun je dat dan wel als je bijv a of b weet? en dan uit L en a: b afleiden of uit L en b: a?

bedankt

Peter en Onno
25-4-2017

Antwoord

Hallo Peter en Onno,

Voor het gemak zetten we de ellips rechtop, en het vierkant dus op zijn punt. De halve korte as noem ik a, de halve lange as noem ik b. De ellips kan dan beschreven worden met de vergelijking:



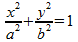
Verder kies ik als zijde van het vierkant L=√2. Dit rekent makkelijk, en voor het resultaat maakt dit niet uit, want achteraf kunnen we altijd schalen.
Wanneer de ellips precies in het vierkant past, dan raakt deze aan de lijn y=-x+1, zie de figuur hieronder.



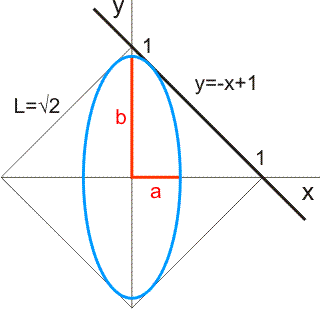
De vraag is nu: welk verband bestaat tussen a en b, in het geval dat de ellips raakt aan de lijn y=-x+1? Om deze vraag te beantwoorden, snijden we de ellips met de rechte. Hiertoe substitueren we y=-x+1 in de vergelijking van de ellips:



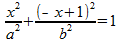
Haakjes wegwerken en op nul herleiden levert de volgende kwadratische vergelijking:



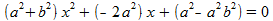
Er is sprake van raken wanneer de discriminant gelijk is aan nul. Wanneer ik geen rekenfout heb gemaakt, levert dit een verrassend eenvoudig verband op:

a²+b²=1

De halve assen a en b zijn evenredig met de zijde van het vierkant, dus voor andere afmetingen van het vierkant kan je eenvoudig opschalen.

OK zo?

GHvD
25-4-2017