We bekijken een driehoek $ABC$ met hoogtepunt $P$. De hoogtelijnen vanuit $A$, $B$ resp. $C$ snijden de overstaande zijde in $D$, $E$ resp. $F$. We spiegelen nu punt $P$ in $F$ en krijgen $P'$. In de figuur is de situatie getekend (met voor het gemak $P$ in het binnenste van de driehoek).
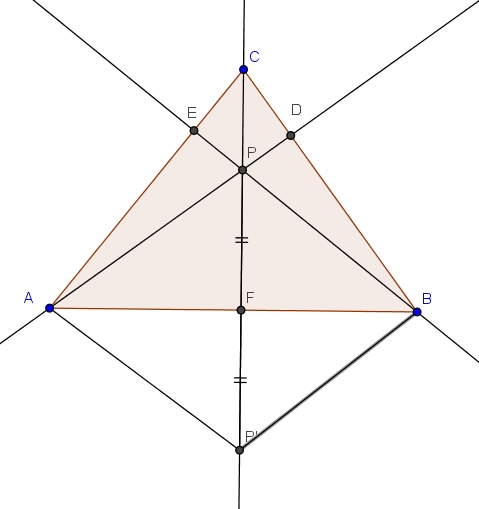
Merk nu op dat $\Delta AFP \sim \Delta ADB$ (hh) en dus $\angle APF = \angle ABC$.
Op dezelfde wijze geldt $\angle BPF = \angle BAC$.
Ook geldt dat $\Delta AFP' \cong \Delta AFP$ en $\Delta BFP' \cong \Delta BFP$ (ZHZ).
Daaruit halen we dat $\angle AP'B = \angle APB = \angle APF + \angle BPF = \angle BAC + \angle ABC = 180^\circ - \angle BCA$.
Daaruit volgt dat $\angle AP'B + \angle BCA = 180^\circ$ en dus is $ABCP'$ een koordenvierhoek, of anders gezegd, ligt $P'$ op de omgeschreven cirkel van $ABC$.
Merk nu op dat $\Delta APB \cong \Delta AP'B$ en dat hun omgeschreven cirkels dus even groot zijn. En we zijn rond.
Met vriendelijke groet,
FvL
5-4-2017