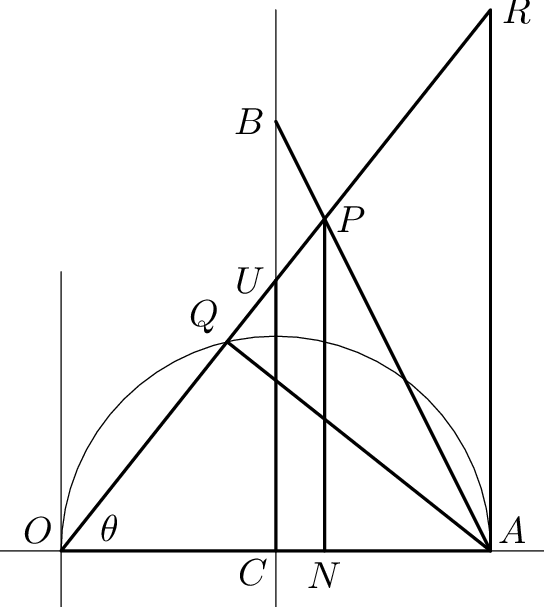
In de berekening op de pagina zijn $x$ en $y$ de coordinaten van $P$ en die zijn dus, respectievelijk $ON$ en $PN$.
De cruciale stap is $OP=OR-OQ$ om te bouwen in termen van $ON$, $PN$, en $OA$.
Er geldt $OR=OA\cdot\frac{OR}{OA}=OA\cdot \frac{OP}{ON}$ en $OQ=OA\cdot{OQ}{OA}=OA\cdot\frac{ON}{OP}$ (denk beide keren aan $\cos\theta$).
Werk nu
$$
OP=OA\left(\frac{OP}{ON}-\frac{ON}{OP}\right)
$$
uit. Dit leidt tot
$$
PN^2=\frac{ON^3}{NA}
$$
en vanaf dat moment gaat alles netjes `planimetrisch'.
kphart
16-3-2017