WisFaq!

Re: De oppervlakte en inhoud van een tetraëder

Hallo,

Ik had een vraag over het gedeelte van uw uitleg:
Nu nog PS berekenen. Met behulp van het gegeven dat ABQ gelijkvormig is met ASP (ga na!) kan je PS berekenen.
PS=1/6·a·√3

Ik kom niet op de 1/6.

Is dit 1/2·1/3=1/6.?
Mar dit doe je toch al in de vervolgstap?

Wanneer ik een verhoudingstabel maak, krijg ik:
AP·BQ/AQ=PS
1/2a·1/2a gedeelt door 1/2a√3=1/2a√3

Hoe bereken ik de 1/6?

Bij voorbaat mijn dank.
Groet Kees

Kees
14-1-2017

Antwoord

Volgens mij krijg je inderdaad:



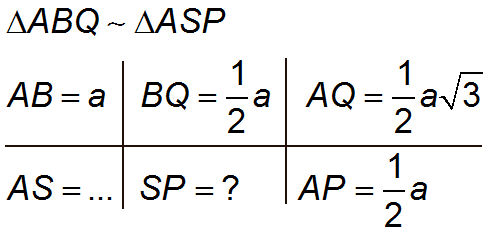
Maar dan:

$
\eqalign{
& SP \cdot \frac{1}
{2}a\sqrt 3 = \frac{1}
{2}a \cdot \frac{1}
{2}a \cr
& SP = \frac{{\frac{1}
{4}a^2 }}
{{\frac{1}
{2}a\sqrt 3 }} = \frac{{a^2 }}
{{2a\sqrt 3 }} = \frac{a}
{{2\sqrt 3 }} \cr
& SP = \frac{a}
{{2\sqrt 3 }} \cdot \frac{{\sqrt 3 }}
{{\sqrt 3 }} = \frac{{a\sqrt 3 }}
{{2 \cdot 3}} = \frac{{a\sqrt 3 }}
{6} = \frac{1}
{6}a\sqrt 3 \cr}
$

...en dat is het dan!

WvR
14-1-2017