1)
Een hypothese is een bewering die waar kan zijn of niet waar kan zijn. =1000 en $>$1000 zijn geen beweringen. Ik denk dat je voor de nulhypothese en alternatieve hypothese bedoelt:
$\mu$ = 1000
$\mu$ $>$ 1000
Dan is dit correct.
2)
Belangrijke tip: maak bij opgaven over de normaalverdeling altijd een schets, zodat je ziet of je berekening past bij de vraag. Deze schets is al goed genoeg:
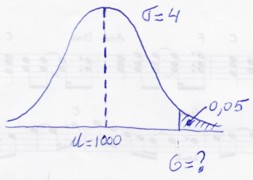
Het gearceerde gedeelte is het kritiek gebied. Dat wil zeggen: wanneer de nulhypothese waar zou zijn, dan is de kans dat het steekproefresultaat in dit kritieke gebied zou vallen kleiner dan het significantieniveau (in dit geval: kleiner dan 0,05). Omdat deze kans zo klein is, nemen we aan dat de nulhypothese onwaar is. De opdracht is: bepaal de grenswaarde G zodat het gebied rechts van G overeenkomt met 0,05.
Jouw invoer in de rekenmachine past bij deze vraag:
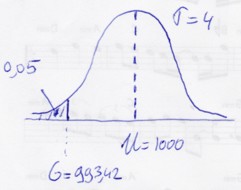
Ofwel: wat is de grenswaarde G zodat het gebied links van G overeenkomt met 0,05? (Immers: de functie InvN berekent een grenswaarde G die behoord bij een gebied links van G). Dat is niet de vraag ....
Wanneer je even doordenkt over jouw antwoord, dan zie je dat dit niet kan kloppen. Immers: de correcte waarde van het gemiddelde is 1000. Volgens jou ligt deze waarde in het kritieke gebied. Dat zou betekenen: wanneer het gemiddelde van jouw steekproef precies 1000 zou zijn, dan zou jij concluderen dat het gemiddelde niet 1000 is. Dat kan toch niet de bedoeling zijn ....
3)
Voor deze vraag hoef je geen nieuwe berekening uit te voeren. Bekijk of het resultaat van de steekproef wel of niet in het kritieke gebied ligt. Op grond daarvan besluit je de nulhypothese te verwerpen dan wel aan te nemen.
4)
Dit is niet dezelfde vraag als 3: de handelaar beweert niet dat de pakken gemiddeld te licht zijn of te zwaar. Hier past dus een tweezijdige toets bij: verdeel het kritieke gebied over twee delen, behorend bij te licht en behorend bij te zwaar.
GHvD
5-6-2016