WisFaq!

Een trimmer op het strand

Wij hebben een probleemstelling waar we niet uit komen:

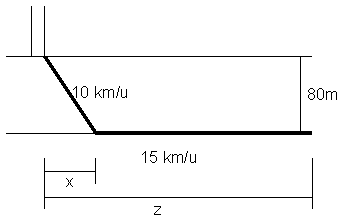
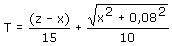Een trimmer loopt over het strand. Hij loopt over het harde zand langs de vloedlijn. in de verte ziet hij de duinovergang waar hij over moet. Als hij schuin het mulle zand oversteekt, legt hij minder grote afstand af dan wanneer hij helemaal doorloopt over het harde zand tot ter hoogte van de duinovergang en dan dwars oversteekt.
Maar op het mulle zand is zijn snelheid kleiner dan op het harde zand. Er is een route die hem het snelst naar de duinovergang zal voeren. De vraag is hoeveel meter voor de duinovergang hij dan het mulle zand op moet gaan.
Neem aan dat de trimmer op het harde zand 15 km/h kan lopen en door het mulle zand 10 km/h. Neem verder aan dat de breedte van het mulle zand 80 meter is. Bereken voor deze situatie hoeveel meter voor de duinovergang hij het mulle zand op moet gaan om zo snel mogelijk bij de duinovergang moet komen. Maak hierbij gebruik van de differentiaalrekening.

Wij hebben al een formule kunnen opstellen:
t=(x/4,17)+(((z-x)²+80²))/2,78
z=totale afstand

Timo van der Heiden
17-12-2001

Antwoord

Eerst maar eens een tekening:



Vervolgens kan je inderdaad een formule opstellen voor de tijd die je nodig hebt...
De keuze voor 'mijn variabele' x haal ik direct uit de vraagstelling: "hoeveel meter voor de duinovergang hij het mulle zand op moet gaan?"
En waarom zouden we niet rekenen in kilometers per uur? (dat is een stuk handiger)
Je krijgt dan:


Wanneer is deze T minimaal?
Afgeleide... (die z is een constante en valt weg?), nul stellen..., tekenverloop... en het zou moeten lukken!

WvR
17-12-2001