WisFaq!

Stroomsterkte in een stroomkring

Voor de stroomsterkte in een stroomkring geldt

I= Asin(wt)+Bcos(wt)
Gevraagt wordt het absolute maximum van I.
De afgeleide I'= Acos(wt)-Bsin(wt) , maar hoe moet het dan verder, sin en cos door de t-formules vervangen met t=tg(y/2) ??? Ik heb het al geprobeerd en het komt niet uit op 'wortel (A²+B²)' want dat is de oplossing volgens het boek. Hoe moet het dan ?

berten
2-3-2003

Antwoord

Met I(t)=A·sin(w·t)+B·cos(w·t) krijg je als afgeleide:
I'(t)=A·w·cos(wt)-B·w·sin(wt)

Nu moet gelden:
A·w·cos(wt)-B·w·sin(wt)=0
A·w·cos(wt)=B·w·sin(wt)
A·cos(wt)=B·sin(wt)
sin(wt)/cos(wt)=A/B
tan(wt)=A/B
wt=arctan(A/B)
t=arctan(A/B)/w

Vul dit in bij I(t)=A·sin(w·t)+B·cos(w·t)

I(t)=A·sin(w·arctan(A/B)/w)+B·cos(w·arctan(A/B)/w)
I(t)=A·sin(arctan(A/B))+B·cos(arctan(A/B))

Maar dan? Wat is nu de sin(arctan(A/B))?
In deze driehoek:



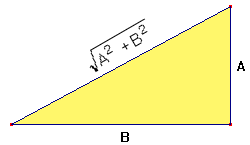
Je kunt dan 'afleiden' dat de sin(arctan(A/B))=A/Ö(A²+B²) en dat cos(arctan(A/B))=BÖ(A²+B²). De rest volgt dan bijna vanzelf:



... hoewel dit vast ook anders (en handiger!) kan. Wat denk je is dit wat je wilt?

WvR
2-3-2003