WisFaq!

Een (on)oplosbare logaritmische vergelijking?

Ik heb hier al flink mee gestoeid, maar ik kom er maar niet uit. Mijn kennis hierover is flink weggezakt.

2·logx = 4·log(3x+4)

Verder dan:

logx²=log(3x+4)²
x²=(3x+4)²

kom ik niet, want ik krijg dit niet opgelost. Misschien pak ik het verkeerd aan. Of misschien is deze wel helemaal niet oplosbaar. Misschien kan ik de log(3x+4) misschien ook anders noteren? Ik weet 't niet!

Kan iemand mij helpen?!
Vr. Groet,
MT

Mike
28-2-2003

Antwoord

Hoi,

2·log(x) = 4·log(3x + 4)
log(x) = 2·log(3x + 4)
log(x) = log(3x + 4)²
x = (3x + 4)²
x = 9x² + 24x + 16
9x² + 24x + 16 - x = 0
9x² + 23x + 16 = 0

Dit laatste kun je oplossen met de abc-formule.
D = b² - 4ac Þ D = 23² - (4·9·16) = -47
De discriminant is kleiner dan 0, dus er zijn geen reële oplossingen. De complexe oplossingen zijn:


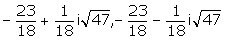
Groetjes,

Davy
28-2-2003