WisFaq!

Cilinder

Bij een holle cilinder met bekende buitendiameter en wanddikte is, vanuit het middelpunt gezien, de doorlopen wanddikte altijd gelijk. Als het punt niet gelijk is aan het middelpunt en men wijkt af van de lijn door het middelpunt, neemt de dikte toe. Zie bijgevoegde schets.

Ik ben op zoek naar een of meerdere formules waarmee is uit te rekenen wat over de omtrek gezien de afstand is tot het punt waarbij de dikte met een bepaalde factor is toegenomen.

Vast bedankt.

jo
18-3-2016

Antwoord

Hallo Jo,

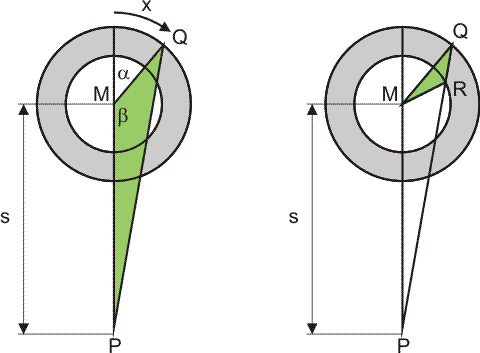
Als ik het goed begrijp, wil je in de rechter figuur hieronder het lijnstuk QR berekenen: de dikte van het materiaal, gezien vanuit een punt P buiten een pijp. De buitendiameter is D, de binnendiameter is d.



Dit kan je als volgt aanpakken:

In de linker figuur is de hoek $\alpha$ gelijk aan x/(D/2) radialen. Hoek $\beta$ is dan $\pi$-$\alpha$. In de groene driehoek PMQ zijn de zijden PM en MQ bekend. Met de cosinusregel bereken je PQ, vervolgens bereken je hoek Q met de cosinusregel of de sinusregel.

In de groene driehoek rechts (MQR) weet je hoek Q en de zijden MQ en MR. Bereken nu QR met opnieuw de cosinusregel.

GHvD
19-3-2016