WisFaq!

Re: Re: Re: Re: Samengestelde Logaritme invoeren in GRM

Nee, daar heb ik geen antwoord op....

Ingrid geerts
4-3-2016

Antwoord

Als je GR geen apart knopje heeft voor een logaritme met een willekeurig grondtal dan maak je gebruik je:

$
\eqalign{{}^g\log (x) = \frac{{\log (x)}}
{{\log (g)}}}
$

In eerste instantie dacht ik dat handig te kunnen doen met:

$
\eqalign{\frac{{\log \left( {\log \left( {\log \left( {\frac{1}
{\pi }} \right)} \right)} \right)}}
{{\log \left( {\frac{1}
{2}} \right) \cdot \log \left( {\frac{1}
{3}} \right) \cdot \log \left( {\frac{1}
{4}} \right)}}}
$

Maar dan gaat niet omdat $
\eqalign{{\log \left( {\frac{1}
{\pi }} \right)}}
$ negatief wordt en dan kan je geen logaritme meer nemen en dan houd het op.

Dit kan je voorkomen door gebruik te maken van:

$
\eqalign{\log \frac{{\left( {\log \frac{{\left( {\frac{{\log \left( {\frac{1}
{\pi }} \right)}}
{{\log \left( {\frac{1}
{4}} \right)}}} \right)}}
{{\log \left( {\frac{1}
{3}} \right)}}} \right)}}
{{\log \left( {\frac{1}
{2}} \right)}}}
$

...en dan werkt het wel...

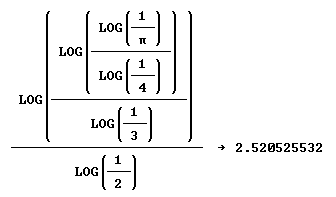
In Derive geeft

log(log(log(1/$\pi$)/log(1/4))/log(1/3))/log(1/2)$\approx$2,520525532

WvR
4-3-2016