Wanneer ik een schets maak van uitslagen van een piramide, lijkt het geen zin te hebben om scheve piramides te maken. Volgens mij is dit de manier om een piramide met een zo groot mogelijke inhoud uit een A4-tje te halen:
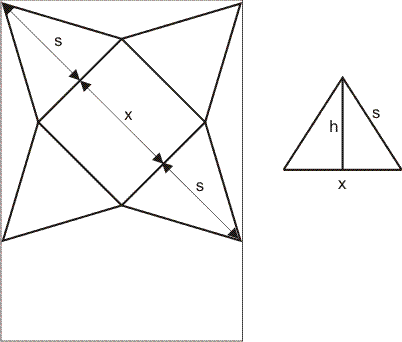
x is de zijde van het vierkante grondvlak, s is de afstand van het midden van een zijde van het grondvlak tot de top. Rechts zie je het vooraanzicht van de piramide die je dan kan maken. De hoogte h van de piramide bereken je met Pythagoras:
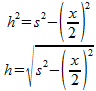
De inhoud van een piramide bereken je met:
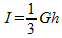
Waarin G de oppervlakte is van het grondvlak. In ons geval is deze oppervlakte gelijk aan x2. Wanneer we G en h in de formule invullen, krijgen we:
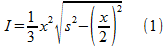
In mijn tekening zie je dat we van het A4-tje maar een vierkant deel gebruiken. De diagonaal van dit vierkant noem ik D. In de tekening zie je dan:
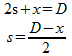
Dit kan je invullen in formule (1). Deze wordt dan:
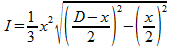
Nu hoef je alleen nog maar de waarde van D in te vullen (korte zijde van een A4-tje, vermenigvuldigd met √2) en het maximum van deze formule te bepalen. In principe kan je dit vinden door de afgeleide te bepalen en deze gelijk te stellen aan nul, maar dat ziet er ingewikkeld uit. Je kan het maximum ook met je GR bepalen.
Lukt het hiermee?
GHvD
26-1-2016