WisFaq!

Hoek tussen twee zwaartelijnen in een tetraëder

Bewijs dat de hoek tussen twee zwaartelijnen in een tetraëder gelijk is aan 109,5° door gerbuik te maken van de driehoeksmeetkunde? Ik weet niet zo goed hoe ik hieraan moet beginnen. Ik dacht wel dat je kon gebruiken dat de zijvlakken van een tetraëder gelijkzijdige driehoeken zijn. En het feit dat het zwaartepunt op de as ligt van de top van de tetraëder naar de grond. Maar hoe je kan berekenen dat deze hoek exact gelijk is aan 109,5° is mij nog onbekend. Alvast bedankt voor de reacties op deze vraag.

Jonas
5-1-2016

Antwoord

Hallo Jonas,

Bekijk maar eens een symmetrievlak in een tetraëder zoals ik dit hieronder heb getekend:



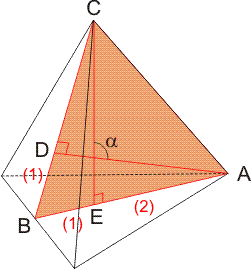
Vanuit de hoekpunten A en C heb ik loodlijnen getrokken naar de tegenoverliggende vlakken. E en D zijn de zwaartepunten van deze vlakken (lukt het je om dit te bewijzen?). De getallen (1) en (2) geven verhoudingen aan van de lijnstukken BD, BE en EA.
In driehoek ABD is hoek B nu te berekenen: cos(B)=1/3. Dit is de hoek tussen twee zwaartelijnen van twee vlakken van de tetraëder. Hiermee zou jouw vraag beantwoord zijn, maar ik vermoed dat je hoek alfa wilt berekenen. Wanneer je hoek B weet, is dit niet meer zo lastig. Wanneer ik het snijpunt van mijn loodlijnen Z noem (dit is het zwaartepunt van de tetraëder), dan is EBDZ een vierhoek waarvan je drie hoeken kent. De som van de vier hoeken is 360°, alfa is dus 360-(B+90+90).
Overigens is deze hoek niet exact 109,5°...

GHvD
6-1-2016