WisFaq!

De kans op getallen in getallen

Ik maak een profielwerkstuk over pi, ik moet alleen de volgende vraag beantwoordden. Wat zijn de kansen dat je bepaalde cijfercombinatie’s terug vindt binnen het getal Pi ? ter verduidelijking: wat is dus de kans dat je een bepaald getal, met lengte N, vindt in een rij van # decimalen, als we aannemen dat Pi een willekeurig getal is.
http://www.angio.net/pi/piquery
Volgens deze site was de formule om dit te berekenen het volgende:

p=kans
N=lengte van het getal
#=aantal decimalen waarin we zoeken

p=1 - (1 - (.1^N))^#

en dan in procenten

p=(1 - (1 - (.1^N))^#))*100%

Maar klopt dit? En zo ja, waarom dan? Zo nee, wat is de formule dan wel?
(owja, ik kom er dus echt niet uit [:S].)
B.v.d.

Toelichting:
I assumed pi is random. The odds of matching the first digit are ¹/₁₀, the second ¹/₁₀, and so on. The odds that any particular string are:

• odds that it exists in one spot: 0.1^N (where N is the length)
• odds that it doesn't exist at that spot: 1 - (0.1^N)
• odds that it doesn't exist at any spot: (1 - (0.1^N))^#digits
• odds that it does exist: 1 - (1 - (0.1^N))^#digits)

So with a string of 8 characters and 100 million digits of pi:

• odds that it exists in one spot: 0.1^N (where N is the length)
• odds that it doesn't exist at that spot: 1 - (0.1^N)
• odds that it doesn't exist at any spot: (1 - (0.1^N))^#digits
• odds that it does exist: 1 - (1 - (0.1^N))^#digits)

and so on....

hugo
18-2-2003

Antwoord

Hallo Hugo, sorry dat je zo lang moest wachten. Het is geen gemakkelijke vraag waar je mee komt. Maar er kan wat mee gedaan worden.

Je twijfelde eraan of de formule die je gevonden had wel goed was. Die twijfel is terecht. De formule is fout. Alleen als N=1 is ie goed. Met een eenvoudig voorbeeld (N en L kleine getallen) kun je al zien dat het niet klopt. En dat er zelfs niet eens een goede formule voor die kans bestaat. Dat gaan we eerst bekijken. Daarna iets positiefs: Voor de verwachting van het aantal keren dat het getal voorkomt is er wel een eenvoudige formule die altijd goed is.

Waar ging het ook weer over?
Je hebt een rij van L cijfers: R=a₁, a₂, ..., a_L , een toevallige rij, d.w.z. zo'n rij die je zou krijgen door L keer met een 10-kantige dobbelsteen te gooien. Je hebt ook een getal G van N cijfers (waarbij natuurlijk N L). Hoe groot is de kans dat G minstens één keer in R voorkomt?
(Vb.Het getal G = 11 komt 3 keer voor in R =341156111731 en wel op plaats 3 en op plaatsen 7 en 8. En 101 komt 2 keer voor in 31010172, op plaats 2 en 4.>

Voorbeeld
Neem nu een eenvoudig voorbeeld : N = 3 en L = 5

1. de kans dat 123 voorkomt in R = abcde. (NB er zijn 100.000 mogelijkheden voor R)
   123 kan hoogstens één keer voorkomen!
   Dat is het geval als:
   R = 123de (100 mogelijkheden)
   Of als R = a123e (100 mogelijkheden)
   Of als R = ab123 (100 mogelijkheden)
   Conclusie: de kans dat 123 voorkomt in R is P = 300/100000 = 0,003
   
   
2. het getal 313 kan 0, 1 of 2 keer voorkomen in R
   1 keer als R = 313de, met de¹13 ( 99 mogelijkheden)
   of als R = a313e (100 mogelijkheden)
   of als R = ab313 met ab¹31 ( 99 mogelijk heden)
   Dus de kans dat 313 1 keer voorkomt P1 = 298/100.000.
   313 kan ook 2 keer voorkomen. Alleen bij R=31313 is dat het geval.
   Dus P2 = 1/100.000
   Conclusie de kans dat 313 voorkomt P=P1+P2=299/100.000.
   
   
3. Het getal 777 kan 0, 1, 2 of zelfs 3 keer voorkomen. En je kunt gemakkelijk de kansen vinden P1 = 261/100000, P2 = 18/100000, P3 =1/100000.
   Dus de kans dat 777 (minstens een keer) voorkomt is 280/100000
   

De kans dat een getal G voorkomt in een rij R hangt dus af van welk getal G je bekijkt. Dus is er geen algemene formule mogelijk die voor alle getallen G zou gelden.

Maar nu het positieve. Als je met behulp van de gevonden kansen de verwachting uitrekent van X, het aantal keer dat G voorkomt in R dan vinden we:
E(X) = P1 + 2·P2 + 3·P3 = 300/100.000 voor 123, 323 en 777.

En we kunnen nu gemakkelijk E(X) bepalen in het algemene geval van een getal van N cijfers in een rij van L cijfers.

We kunnen X bepalen door te tellen of het getal G op plaats 1 staat (dwz de eerste N cijfers van R)
Schrijf X1=1 als dit zo is en X1=0 als dit niet zo is. X2 geeft op dezelfde manier aan of G voorkomt op plaats 2 (dwz 1 plaats opgeschoven vanaf het begin van R ).
Zodoende krijg je X = X1 + X2 + ... + Xk ( met k = L - N + 1)
Gebruik nu de opteleigenschap voor de verwachting:
E(X) = E(X1 + X2 + ... + Xk) = E(X1) + E(X2) + ... +E(Xk) = k·E(X1) = k/10^N.
Dus:

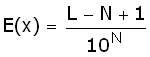
En deze formule is altijd goed.

En nog iets. Als E(X) klein is dan is P1 ook klein en P2 nog veel kleiner, zodat dan, wegens E(X)= P1 + 2P2 +... bijna gelijk is aan P = P1 + P2 +...
Dit is het geval als L veel kleiner is dan 10^N

Ik hoop dat je met dit antwoord tevreden bent. Veel succes met je onderzoek.

P.S.
Je wilt mischien nog weten waarom de formule die je op internet gevonden had fout is. Dat komt omdat er geen rekening is gehouden met de afhankelijkheid die er is tussen het voorkomen van het getal op plaatsen dicht bij elkaar. Ze doen net alsof bijvoorbeeld de gebeurtenis A1:"het getal 123 staat op plaats 1" en A2:"het getal staat op plaats 2" onafhankelijke gebeurtenissen zijn. Dan zou moeten gelden P(A1 en A2)=P(A1)·P(A2)=1/1000.000. Maar dat is dus niet zo.

JCS
1-3-2003