Waarschijnlijk ken je de volgende vuistregels:
- Tussen $\mu$-$\sigma$ en $\mu$+$\sigma$ ligt ongeveer 68% van de oppervlakte onder de normaalkromme,
- Tussen $\mu$-2$\sigma$ en $\mu$+2$\sigma$ ligt ongeveer 95% van de oppervlakte onder de normaalkromme.
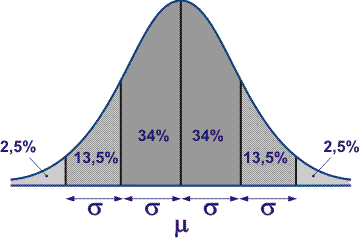
Aan de hand van enkele voorbeelden laat ik zien hoe je deze vuistregels kunt gebruiken om de standaardafwijking te schatten:
Voorbeeld 1:
Gegeven: gemiddelde is 40, 25% van de waarden ligt boven 42.
Gevraagd: de standaardafwijking.
Maak altijd een schets met daarin de gegevens:
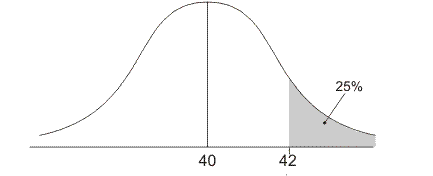
De afstand tussen gemiddelde en grenswaarde is 2. 25% van de oppervlakte onder de curve ligt rechts van de grenswaarde 42. Volgens de vuistregels ligt deze grenswaarde dan minder dan één keer de standaardafwijking rechts van het gemiddelde. De standaardafwijking is zodoende kleiner dan 2. Kies bijvoorbeeld XMIN=0 en XMAX=3, dan vind je de standaardafwijking zeker binnen je venster.
Voorbeeld 2:
Gegeven: gemiddelde is 7, 8% van de waarden ligt onder 5,5.
Gevraagd: de standaardafwijking.
Maak een schets met daarin de gegevens:
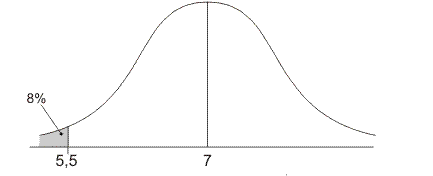
De afstand tussen grenswaarde en gemiddelde is 1,5. 8% van de oppervlakte onder de curve ligt links van deze grenswaarde. Volgens de vuistregels is deze afstand van 1,5 dan groter dan één keer de standaardafwijking, maar kleiner dan twee keer de standaardafwijking. De standaardafwijking ligt zodoende tussen 1,5 en 3. Kies XMIN=1,5 (of nog wat kleiner) en XMAX=3 (of nog wat groter), dan vind je de standaardafwijking zeker binnen je venster.
Voorbeeld 3:
Gegeven: standaardafwijking is 10, 20% van de waarden ligt boven 70.
Gevraagd: het gemiddelde.
Maak een schets met daarin de gegevens:
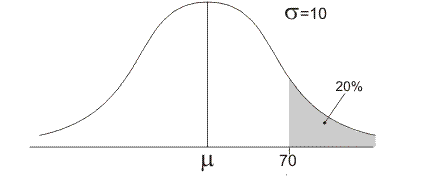
20% van de oppervlakte ligt rechts van de grenswaarde 70. Volgens de vuistregels ligt deze grenswaarde dan minder dan één keer de standaardafwijking verwijderd van het gemiddelde. Het gemiddelde is dus groter dan (70-10)=60, maar zeker kleiner dan de grenswaarde 70. Met XMIN=60 en XMAX=70 moet je gemiddelde binnen je venster liggen.
Voorbeeld 4:
Gegeven: standaardafwijking is 10, 8% van de waarden ligt onder 5,5.
Gevraagd: het gemiddelde.
Maak een schets met daarin de gegevens:
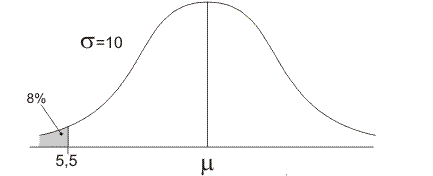
8% van de oppervlakte ligt links van de grenswaarde 5,5. Volgens de vuistregels ligt deze grenswaarde meer dan één keer de standaardafwijking verwijderd van het gemiddelde, maar minder dan twee keer de standaardafwijking. Het gemiddelde is dus meer dan (5,5+10)=15, maar minder dan (5,5+20)=25. Met XMIN=15 en XMAX=25 moet je gemiddelde binnen je venster liggen.
OK zo?
GHvD
16-12-2015