WisFaq!

Vraagstuk waarbij de parameters b en c bepaald moeten worden aan de hand van as

Ik ben aan het oefenen voor een toets wiskunde en de leerkracht had enkele goede oefeningen voor thuis meegegeven. Ik ben eraan begonnen maar er is 1 oefening die ik echt niet kan vinden.

De opdracht is:

Beschouw de functie met voorschrift f(x) = Ln( e/(e^(bx)-c)) met b en c twee parameters strikt groter dan 0.

Bepaal de waarde voor b en c zodanig dat het domein van de functie ]-3, +OO[ en zodanig dat de grafiek als verticale asymptoot de rechte met vergelijking x=-3 en als schuine asymptoot de rechte met vergelijking y=-3x+1 heeft.

Thomas
11-11-2015

Antwoord

Hallo Thomas,

We kunnen je functie herschrijven tot:

f(x) = Ln(e) - Ln(e^bx-c)
f(x) = 1 - Ln(e^bx-c)

Wanneer deze functie voor x-$>$oneindig een schuine asymptoot heeft met vergelijking y=-3x+1, dan wordt het verschil f(x)-y nul wanneer x naar oneindig gaat. Dus:



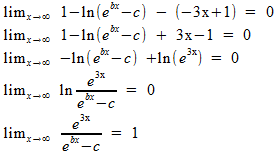
Hieruit volgt: b=3 (leid dit zelf verder af)

We weten nu:
f(x)= 1 - Ln(e^3x-c)

Een Ln-functie heeft een verticale asymptoot waar het argument gelijk wordt aan nul. De vericale asymptoot verwacht je dus wanneer:

e^3x-c=0

De eis is dat je een verticale asymptoot vindt bij x=-3. Met bovenstaande vergelijking is c dan te berekenen.

GHvD
11-11-2015