WisFaq!

De standaaarddeviatie berekenen

In een distributie met gemiddelde=50 een score van X=42 correspondeert met een z-score van -2,00. Wat is de standaardafwijking van deze distributie (verdeling).

Ik moet dan de volgende formule invullen:
z=X-mu/standaardafwijking (formule voor z-scores).

Je kan deze formule ook anders schrijven als je de X score wil weten: X=mu(gemiddelde)+z x standaardafwijking

Het probleem is dat ik nu de standaardafwijking moet vinden en ik weet niet hoe ik die kan uitrekenen.

• Statistiek en kansrekenen

yalda
26-10-2015

Antwoord

Er geldt:

$
\eqalign{z = \frac{{x - \mu }}
{\sigma }}
$

Invullen geeft:

$
\eqalign{
& - 2,00 = \frac{{42 - 50}}
{\sigma } \cr
& - 2,00 = \frac{{ - 8}}
{\sigma } \cr}
$

Denk maar aan:



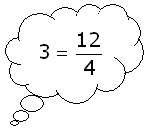
Wat moet je doen om $4$ te vinden? Je moet dan $12$ delen door $3$, dus in jouw geval wordt dat:

$
\eqalign{
& - 2,00 = \frac{{42 - 50}}
{\sigma } \cr
& - 2,00 = \frac{{ - 8}}
{\sigma } \cr
& \sigma = \frac{{ - 8}}
{{ - 2,00}} = 4 \cr}
$

Waarmee dit probleem weer is opgelost...

WvR
26-10-2015