WisFaq!

Drukstijging door temp VS drukdaling door lek

Beste,

Hierbij een probleem wat gaat over de druk in een bepaalde ruimte.

De ruimte wordt verwarmd wat zorgt voor een drukstijging. Door deze drukstijging treedt er lekkage op want de ruimte is niet 100% dicht.

Getallen:
Volume ruimte: 420.000 m3
Temp. stijging: 50K in 2,5 uur
Lekkage: 17 m3/min per √Pa drukverschil

als ik het goed heb:
dP/dt = drukstijging door temp. toename - drukdaling door lekkage.

Stel dat de ruimte niet lek is, dan stijgt de druk met ca. 18.000 Pa in 2,5 uur. Als dit linear gebeurt is dat dus 120 Pa per minuut.

De daling is afhankelijk van de druk zelf: Er stroomt een volume uit de ruimte van √P(t)·17. Hier zit een bepaald aantal mol in wat de ruimte uitstroomt. In de ruimte zitten nu dus minder molen dan daarvoor, wat moet worden omgezet in een equivalente drukdaling. Hier loop ik op vast.

Is er iemand die hier natuurkundig en/of wiskundig mee kan helpen? Het liefste maak ik een grafiek van het drukverloop in de ruimte vanaf t=0 naar t = 4 uur.

Arnout
23-9-2015

Antwoord

Hallo Arnout,

Het lijkt mij het handigst om een formule te zoeken die het aantal mol gas in de ruimte beschrijft. Laten we eerst eens kijken naar de lek. Deze bedraagt 17 m³ per minuut per √drukverschil. Het aantal mol gas in 17 m³ is echter niet constant. Ik neem aan dat je bedoelt: 17 m³ onder de omstandigheden zoals deze op dat moment in de afgesloten ruimte zijn. Dat betekent dat er 17/420000-ste deel van het totale volume wegstroomt per minuut per √drukverschil. Dan stroomt er per minuut per √drukverschil ook 17/420000-ste deel van het aantal moleculen weg dat op dat moment nog aanwezig is. In formule:



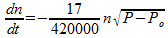
Hierin is:
n = aantal mol gas in de ruimte
t = tijd in minuten
P = absolute druk in de ruimte (in Pa)
P_o = omgevingsdruk (in Pa)

Vervolgens bedenken we dat in de bedoelde ruimte altijd geldt:

P·V = n·R·T (algemene gaswet) ofwel:

P = ^n·R/_V·T

Hierin is:
V = volume van de ruimte (= constant, 420000 m³)
R = algemene gasconstante (8,3144621 J/K/mol)
T = temperatuur van het gas in de ruimte (in Kelvin)

Ik begrijp dat de temperatuur gelijkmatig stijgt met 50 K per 2,5 uur, dus ¹/₃ K/minuut. Voor de temperatuur T geldt dan:

T = T₀+¹/₃t

Hierin is:
T₀ = temperatuur op tijdstip t=0 (in Kelvin).

Substitutie in de algemene gaswet levert:



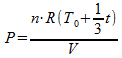
Dit kunnen we weer substitueren in de eerste vergelijking:



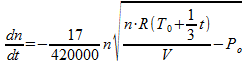
Deze differentiaalvergelijking beschrijft het verloop van het aantal mol gas in de ruimte (n) in de tijd (t). De vergelijking is denk ik niet analytisch op te lossen, maar een geschikt simulatieprogramma zou dit verloop wel moeten kunnen berekenen. Het verloop van de druk vind je dan weer door de berekende waarden van n in de vorige formule in te vullen.

Ik hoop dat ik niets over het hoofd heb gezien.

GHvD
24-9-2015