WisFaq!

Ongelijkheden oplossen

Hallo,

Ik loop altijd aan tegen het probleem dat ik er niet uitkom met ongelijkheden oplossen (vooral als er een breuk in voorkomt). Ik weet dat je waarschijnlijk gebruik moet maken van een tekenschema, maar ik ben hier totaal niet bekend mee.

Vraag 1:
Als je de teller en noemer van de breuk eerst uitschrijft in een tekenschema, en deze daarna combineert, mag je dan gewoon de twee tekenschema's 'combineren' in de derde zeg maar? Of moet je altijd in de formule kijken wanneer het positief/negatief moet zijn?

Vraag 2:
Een voorbeeld waar ik niet uit kom is de volgende:

$\eqalign{\frac{{11x + 8}}{{2x + 3}} \gt 6}$

Zou u dit in duidelijke stappen uit kunnen leggen? (Vooral wat betreft het tekenschema dan).

Alvast bedankt!!

Groetjes Julia

Julia
7-9-2015

Antwoord

Je moet eerst op nul herleiden en de zaak onder één noemer zetten.

$
\eqalign{
& \frac{{11x + 8}}
{{2x + 3}} \gt 6 \cr
& \frac{{11x + 8}}
{{2x + 3}} - 6 \gt 0 \cr
& \frac{{11x + 8}}
{{2x + 3}} - \frac{{6 \cdot \left( {2x + 3} \right)}}
{{2x + 3}} \gt 0 \cr
& \frac{{11x + 8}}
{{2x + 3}} - \frac{{12x + 18}}
{{2x + 3}} \gt 0 \cr
& \frac{{ - x - 10}}
{{2x + 3}} \gt 0 \cr}
$

Nu kun je naar het tekenverloop van de teller, de noemer en de breuk gaan kijken:



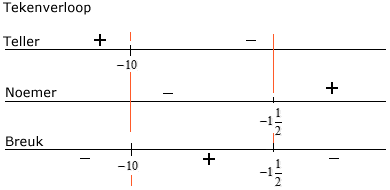
Oplossing: $-10\lt x\lt -1\frac{1}{2}$

• Oplossen van een ongelijkheid
• Een ongelijkheid oplossen
• Een ongelijkheid oplossen in R
• Ongelijkheden breuk oplossen

WvR
7-9-2015