Teken een cirkel rond je silo op de hoogte waar het midden van je zaagsnede moet komen. Let er uiteraard op dat het vlak van deze cirkel mooi haaks staat op de lengte-as van de silo (bijvoorbeeld door vaste hoogtes uit te meten vanaf de bodem, wanneer deze bodem goed haaks is).
Meet de omtrek van je silo. Bij een doorsnede van 190 cm hoort een omtrek van $\pi$.190=596,9 cm. Verdeel deze omtrek in een gewenst aantal gelijke delen. Wanneer je kiest voor 16 punten, is de afstand tussen deze punten 596,9/16=37,3 cm.
Teken vanuit elk van deze punten een lijn evenwijdig aan de lengte-as van je silo, bijvoorbeeld door ook langs de onderrand deze 16 punten uit te zetten en overeenkomende punten te verbinden, zie onderstaande figuur.
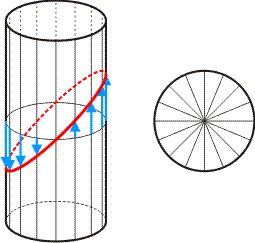
De cirkelvormige doorsnede heb je nu verdeeld in 16 'taartpunten', zie de figuur rechts. De hoek van elke taartpunt bedraagt 360/16=22,5 graden. Langs de verticale lijnen meet je nu hoogtes af waarvoor geldt:
Hoogte = straal x sinus(hoek)
Zie de blauwe pijlen. De straal bedraagt 190/2 = 95 cm. Voor de lengtes van de blauwe pijlen vind je:
pijl nr. 1: 95 x sinus(22,5°) = 95 x 0,383 = 36,4 cm
pijl nr. 2: 95 x sinus(45,0°) = 95 x 0,707 = 67,2 cm
pijl nr. 3: 95 x sinus(67,5°) = 95 x 0,924 = 87,8 cm
pijl nr. 4: 95 x sinus(90,0°) = 95 x 1,000 = 95,0 cm
Deze laatste waarde weet je ook van tevoren: bij zagen onder een hoek van 45° kom je net zo hoog uit als de straal van je silo.
Uiteraard vind je naar links dezelfde waarden naar beneden, en de achterzijde is gelijk aan de voorzijde.
GHvD
2-9-2015