WisFaq!

Aantal ballen in een piramide

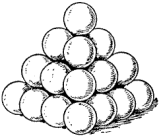
Een piramide met golfballen. Onderste rij 7, op de top 1. totaal dus 140 ballen in de piramide (7²+6²+...).



Is voor een dergelijke reeks een formule om het totaal aantal makkelijker te berekenen? Ik heb geen wiskundig inzicht, maar mijn exact denkende vrienden komen hier ook niet uit.
Dank.

Peter Krom
22-6-2015

Antwoord

$
P_n = \sum\limits_{k = 1}^n {k^2 } = \frac{1}
{6}n\left( {n + 1} \right)\left( {2n + 1} \right)
$

Voor n=7:

$
P_7 = \frac{1}
{6} \cdot 7 \cdot 8 \cdot 15 = 140
$

Je moet maar 's kijken op:

• Square Pyramidal Number

WvR
22-6-2015