WisFaq!

Bewijs oplossen met volledige inductie

Geg: n ϵ N_0
T.B.: 3⁽²ⁿ⁺¹⁾+2^(n-1) is een zevenvoud
ik kan wel 1 invullen, veronderstellen dat het geldt voor k mlaar dan zit ik vast als ik het moet bewijzen voor k+1

jelle
2-5-2015

Antwoord

Hallo Jelle,

Je hebt al gezien dat n=1 een zevenvoud oplevert. Je weet ook al dat we veronderstellen dat dit een zevenvoud is:



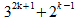
Nu gaan we bekijken wat de formule oplevert wanneer we n=k+1 invullen:



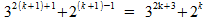
We gaan nu proberen om deze formule op zo'n manier te herleiden dat we de machten van de eerste formule terugkrijgen. We krijgen dan:



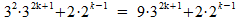
Geheel rechts zien we het rechter deel van de oorspronkelijke formule, vermenigvuldigd met 2. Helaas is het linker deel vermenigvuldigd met 9. Die factor 9 splitsen we op in 7 en 2:



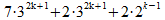
zodat we krijgen:



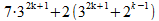
Rechts zien we nu 2 keer de eerste formule. Deze eerste formule is een zevenvoud (dat was de veronderstelling), dan is 2 keer deze formule ook een zevenvoud.
Het linker deel bevat de factor 7, en is dus ook zeker een zevenvoud. het geheel is dan ook een zevenvoud.

GHvD
2-5-2015